Астрономи переконані, що Всесвіт прискорюється. Цей революційний прогрес кидає теоретичній космології величезний визов, на який вона досі не може відповідати.
Пояснення космічного прискорення в рамках загальної теорії відносності Ейнштейна пов'язане з непереборними труднощами. Релятивістські моделі засновані на полі темної енергії з неприродними властивостями. Існує велика різноманітність таких моделей, але всі вони мають одну спільну рису - нездатність врахувати гравітаційні властивості енергії вакууму.
Спекулятивні ідеї з теорії струн пульсують туманними надіями, але переконливої моделі поки що не запропоновано.
Альтернатива темній енергії полягає у припущенні, що сама гравітація може поводитися інакше, ніж стверджує загальна теорія відносності, - у найбільших, космологічних масштабах, зрозуміло. Саме гравітація створює прискорення Всесвіту або те, що астрономи сприймають як розширення воістину глобального матеріального світу.
Альтернативний підхід модифікованої гравітації (або темної гравітації) дає новий кут зору на проблему, але також стикається з серйозними труднощами, включаючи проблему пояснення, чому енергія вакууму не гравітує.
Відсутність адекватної теоретичної основи для прискорення Всесвіту в пізні години є глибоким кризом для теоретичної космології, але це ж і захоплююча загадка для кабінетних учених. Видається ймовірним, що для розв'язання цього кризи знадобиться абсолютно нова парадигма.
1. Вступ
Сучасна "стандартна модель" космології - це інваріантна модель холодної темної матерії з космологічною постійною, яка зазвичай називається LCDM, що базується на загальній відносності та фізиці частинок (тобто Стандартній моделі та її мінімальних суперсиметричних розширеннях).

Подібна модель забезпечує чудову відповідність багатству високоточних даних спостережень на основі надзвичайно малого числа космологічних параметрів [1]. Зокрема, незалежні набори даних з анізотропії космічного мікрохвильового фону (КМФ), оглядів галактик та світності наднових призводять до погодженого набору параметрів, що як би демонструє незаперечний тріумф LCDM.
Стандартна модель напрочуд успішна, але ми знаємо, що її теоретична основа, загальна відносність, руйнується за досить високих енергій, що їх зазвичай приймають за планковську метрику,

Модель LCDM може дати лише обмежене уявлення про дуже ранній Всесвіт.
В свою чергу, квантова теорія гравітації здатна досліджувати більш високі енергії та більш ранні години; за ідеєю, вона повинна забезпечити послідовний фундамент для інфляції або її альтернативи у рамках стандартної космологічної моделі.
Ще більш серйозною теоретичною проблемою, ніж інфляція, є прискорення у пізні часи Всесвіту, що розширюється [3]. З погляду фундаментальних параметрів густини енергії, сучасна космічна енергія представляється таким чином:
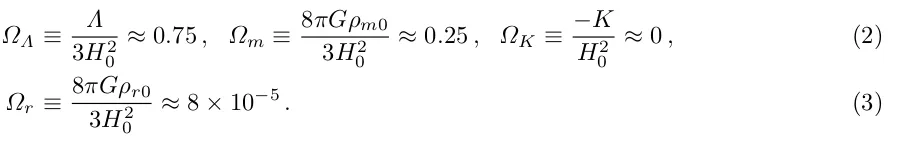
Тут H0 - поточне значення параметра Габбла, Λ - космологічна постійна, K - кривизна, ρm0 - поточна густина матерії та ρr0 - поточна густина випромінювання. G - постійна.
Рівняння Фрідмана має вигляд:
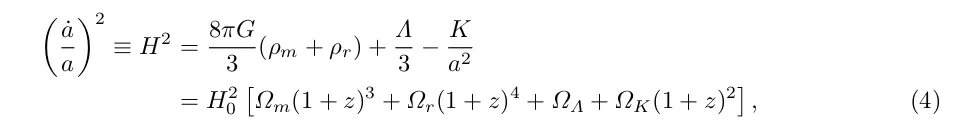
де a позначає метричний фактор (масштаб всесвіту), який пов'язаний із космологічним червоним зміщенням через 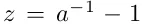 . Ми нормуємо цей масштабний фактор на a0 = 1. Разом із рівнянням збереження енергії це означає, що
. Ми нормуємо цей масштабний фактор на a0 = 1. Разом із рівнянням збереження енергії це означає, що

Спостереження, які разом з Eq (4) приводять до значень, зазначених у рівнянні (5), можуть свідчити про те, що Всесвіт нині прискорюється:

Однак такий висновок справедливий тільки в тому разі, якщо Всесвіт (майже) однорідний та ізотропний, тобто ми маємо справу з моделлю Фрідмана-Леметра.
У цьому разі відстань до заданого червоного зсуву z і час, що минув з моменту виникнення червоного зсуву, тісно пов'язані через єдину вільну функцію цієї геометрії, a(t).
Якщо ж Всесвіт навколо нас ізотропний, але не однорідний, тобто якщо він нагадує розв'язок Толмена-Бонді-Леметра з нашим скупченням галактик у центрі, то цей тісний зв'язок між відстанню і часом для цього червоного зсуву буде втрачено, й отримані дані не обов'язково означають прискорення.
Описаний момент докладно обговорюється в статті Енквіста [4]. Звичайно, ізотропія без однорідності порушує принцип Коперника, оскільки поміщає нас у центр Всесвіту. Однак слід підкреслити, що досі спостереження однорідності дуже обмежені, на відміну від ізотропії, яка твердо встановлена.
Однорідність зазвичай виводиться з ізотропії разом із принципом Коперника. З отриманням майбутніх даних, у принципі, буде можливо спостережливо відрізнити ізотропний, але неоднорідний Всесвіт від ізотропного й однорідного (див., наприклад, [5]). Надалі ми нехтуємо цією можливістю і припускаємо, що принцип Коперника застосовний.
Дані також вказують на те, що Всесвіт нині (майже) просторово плоский.

Зазвичай прийнято вважати, що це передбачає K = 0 за наявності інфляції. Однак інфляція передбачає не K = 0, а тільки 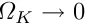 . У пізньому Всесвіті така відмінність може бути незначною. Але на самому початку ненульова кривизна може мати значні ефекти (див., наприклад, [6]).
. У пізньому Всесвіті така відмінність може бути незначною. Але на самому початку ненульова кривизна може мати значні ефекти (див., наприклад, [6]).
Іншими словами, якщо кривизна мала, але не убуває, нехтування нею під час аналізу даних про наднові призводить до катастрофічно великих помилок, як показано в роботі Хлозека та ін. [7].
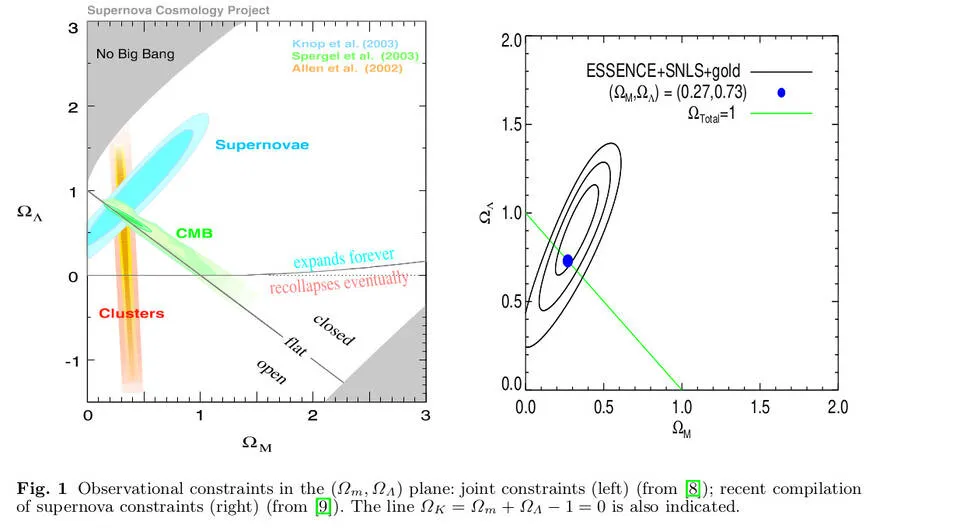
Пропоновані мікровисновки проілюстровано на рис. 1 (взято з [8,9]). Докладне обговорення експериментальних аспектів прискорення в пізні часи наведено в роботах Лейбундгута [10], Ніколя [11] і Саркара [12].
Найпростіший варіант - це, ймовірно, космологічна постійна, тобто модель LCDM. Навіть якщо космологічну постійну можна розглядати як просто додаткову гравітаційну постійну (на додаток до
постійної Ньютона), космологічна постійна входить у рівняння Ейнштейна точно так само, як і енергія вакууму, тобто через лоренц-інваріантний тензор енергії-момента 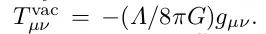 .
.
Єдиною спостережуваною ознакою космологічної сталої і вакуумної енергії є їхній вплив на простір-час, тому вакуумну енергію і космологічну сталу не можна відрізнити одна від одної. Тому "класичне" поняття космологічної сталої фактично не відрізняється від квантової енергії вакууму.
Незважаючи на те, що абсолютне значення енергії вакууму не може бути розраховане в рамках квантової теорії поля, зміни енергії вакууму (наприклад, під час фазового переходу) можуть бути розраховані, і вони справді мають фізичний ефект - наприклад, на енергетичні рівні атомів (зсув Лемба), який добре виміряний.
Крім того, були розраховані відмінності енергії вакууму, наприклад, між двома великими металевими пластинами або на одній з їхніх сторін, а також їхній вплив, сила Казимира[13]. Отже, немає жодних сумнівів у реальності вакуумної енергії.
Для теорії поля зі шкалою енергії відсічення E густина енергії вакууму масштабується з відсіченням як ρ vac ∼ E 4 , що відповідає космологічній постійній Λ vac = ρ vac /(8πG). Якщо E = Mp , це дає перенормування "космологічної постійної" близько Λ vac ∼ 10 38 Гев 2 , тоді як виміряна ефективна космологічна постійна є сумою
"голої" космологічної сталої та внеску від перенормування,
Λ eff = Λ vac + Λ ≃ 10 -83 ГэВ 2
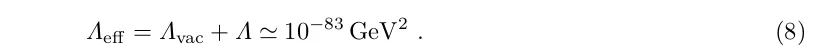
Отже, потрібне скасування приблизно на 120 порядків. Це називається "тонким налаштуванням" або проблемою об'єму темної енергії: скасування необхідне для отримання результату, який на багато порядків менший за кожен із членів. Можливо, що енергія квантового вакууму набагато менша, ніж метрика Планка.
Але навіть якщо ми встановимо її на мінімально можливому масштабі SUSY, E susy ∼ 1TeV, стверджуючи, що за вищих енергій енергія вакууму точно анулюється через суперсиметрію, необхідне анулювання все одно становить близько 60 порядків. Ці питання обговорюються в роботах Падманабхана [14] і Буссо [15].
Розумним ставленням до цієї відкритої проблеми є надія на те, що квантова гравітація пояснить це скасування. Але тоді набагато ймовірніше, що ми отримаємо безпосередньо Λ vac + Λ = 0, а не Λ vac + Λ ≃ 3ρ m (t 0 )/(8πG). Цей несподіваний результат спостережень призводить до другої проблеми - проблеми збігу: враховуючи, що
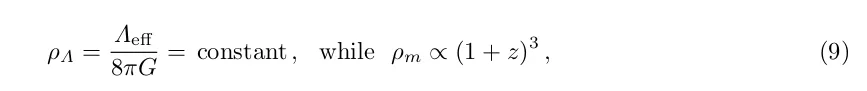
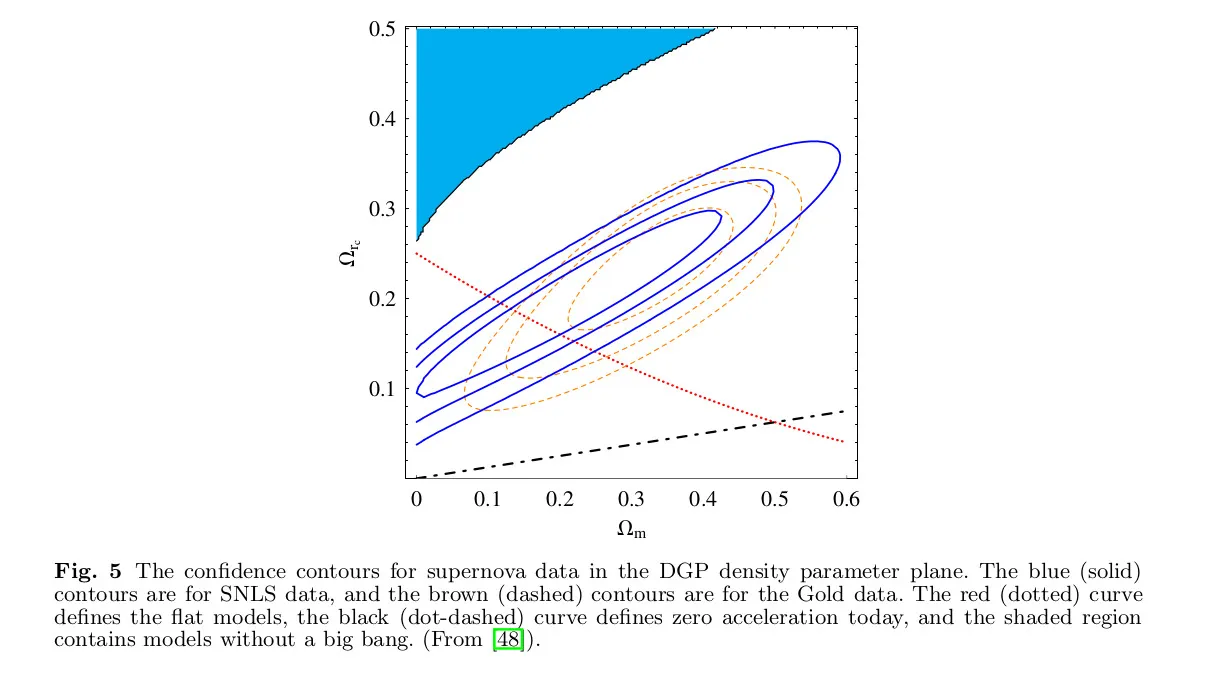
Чому ρ Λ МАЄ порядок нинішньої щільності матерії ρm (t0 )? Вона була абсолютно нікчемною в більшій частині минулого і буде повністю домінувати в майбутньому.
Замість космологічної сталої можна також ввести скалярне поле або будь-який інший елемент у тензор енергії-моменту, який має рівняння стану w < -1/3. Такий компонент називається "темною енергією". Досі не було запропоновано жодної послідовної моделі цього елемента, яка могла б дати природничо-наукове пояснення проблеми, що розглядається. Різноманітність таких моделей обговорюється в статті Ліндера [16].
Як альтернативу припустимо, що поля темної енергії не існує, але натомість прискорення в пізні часи є сигнатурою гравітаційного ефекту. У рамках загальної теорії відносності виникає вимога, щоб вплив неоднорідностей якимось чином призводив до прискорення або появи прискорення (у рамках інтерпретації Фрідмана-Леметра).
Один із можливих варіантів - модель Толмена-Бонді-Леметра, яку обговорювали в [4]. Інша можливість полягає в тому, що "зворотна реакція" неоднорідностей, оброблена за допомогою нелінійного усереднення, створює ефективне прискорення. Далі дивіться припущення Бухерта [17].
Більш радикальним виглядає підхід "темної гравітації" - ідея про те, що сама гравітація ослаблена у великих масштабах, тобто що існує "інфрачервона" модифікація загальної відносності, яка пояснює прискорення в пізні часи. Специфічні класи моделей, що модифікують гравітацію, обговорюються в роботах Капоццієлло і Франкавілья [18] і Коями [19]. Схематично, ми змінюємо геометричну з боку рівнянь поля,

а не з боку матерії,

як у підході загальної теорії відносності.
Модифікована гравітація являє собою інтригуючу можливість для розв'язання теоретичної кризи, викликаної прискоренням пізнього всесвіту. Однак модифікувати загальну теорію відносності Ейнштейна в системах низьких енергій надзвичайно складно, оскільки порушуються обмеження, з ними пов'язані. Попри свою примарність, у космології не існує переконливої альтернативи моделям темної енергії. Виникає логічне коло, з якого теоретична космологія не може вирватися.
Частину цієї роботи, що залишилася, побудовано таким чином.
У розділі 2 ми обговорюємо обмеження, які можна сформулювати для теорії темної енергії або модифікованої гравітації (темної гравітації), виходячи з основних теоретичних вимог.
У розділі 3 ми обговорюємо моделі, які вирішують проблему темної енергії в рамках загальної теорії відносності.
У розділі 4 ми представляємо моделі модифікованої гравітації.
У розділі 5 ми підбиваємо підсумки.
2 Обмеження ефективних теорій
Теорії темної матерії і темної енергії часто мають дуже незвичайні лагранжіани, які не можуть бути квантувані звичайним способом, тому що вони мають нестандартні кінетичні члени. Ми просто називаємо їх "ефективними теоріями низьких енергій", припускаючи наявність більш загальної теорії високих енергій, яку ми не уточнюємо.
У цьому розділі ми хочемо вказати на кілька властивостей ефективних теорій низьких енергій. Спочатку ми перелічимо необхідні властивості базової фізичної теорії на класичному і квантовому рівні. Потім обговоримо, які з цих вимог успадковуються ефективними описами низьких енергій.
2.1 Фундаментальні фізичні теорії
Тут ми наводимо мінімальний список властивостей, які ми вимагаємо від фундаментальної фізичної теорії. Звичайно, всі перераховані нижче пункти відкриті для обговорення, але, принаймні, ми повинні знати, що ми втрачаємо, коли відмовляємося від них.
У нашому списку ми починаємо з найосновніших вимог, які в міру просування стають дедалі суворішими. Незважаючи на те, що деякі теоретики могли б жити без одного або декількох з обговорюваних тут критеріїв, ми вважаємо, що всі вони дуже добре обґрунтовані. Ба більше, всі відомі сучасні фізичні теорії, включно зі струнною і М-теорією, дотримуються їх.
2.1.1 Фізична теорія дає змогу математично описати якусь реальність або те, що ми маємо на увазі під реальністю
Це основна ідея теоретичної фізики. Вона цілком може виявитися помилковою на якомусь етапі, але вона обов'язково проходить крізь етап робочої гіпотези для всього того, що ми називаємо теоретичною фізикою. Якщо в неї є обмеження, їх можна назвати обмеженнями самої теоретичної фізики.
2.1.2 Фізична теорія допускає лагранжеве формулювання
Фундаментальні фізичні теорії мають лагранжеве формулювання. Ця вимога, звісно, набагато сильніша за попередню. Але вона була надзвичайно успішною і тому стала керівним принципом для розвитку квантової теорії поля і теорії струн у 20 столітті.
Якщо ми відмовимося від нього, все піде як по маслу. Тоді ми можемо просто сказати, що еволюція масштабного фактора Всесвіту
описується 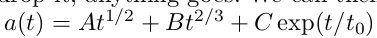 , назвемо це фізичною теорією і підберемо чотири параметри A, B, C і t0 з космологічних даних.
, назвемо це фізичною теорією і підберемо чотири параметри A, B, C і t0 з космологічних даних.
Звісно, більшість аналогових вишукувань не заслуговує на назву "теорія"; це просто підгонка до даних.
Проте іноді до подібних примх ставляться більш серйозно, ніж слід було б. Деякі "теорії мінливої швидкості світла" без лагранжевого формулювання залишають нам більшу або меншу свободу у визначенні еволюції швидкості світла в ході історії розширення Всесвіту.
Утім, якщо ми вводимо формулювання Лагранжа, ми розуміємо, що більшість цих теорій - варіації скалярно-тензорних моделей гравітації, які добре визначено й докладно описано.
Якщо ми хочемо зберегти глибокі фізичні ідеї, такі, як теорема Нотера, що пов'язує симетрію із законами збереження, нам доведеться прописати лагранжеве формулювання фізичної теорії.
Основним інгредієнтом лагранжевої фізичної теорії є розуміння того, що кожен фізичний ступінь свободи має кінетичний член, який зазвичай складається з похідних першого порядку за часом, а також може мати "потенційний член", що не включає похідні.
У лагранжевому формулюванні фундаментальної фізичної теорії ми не допускаємо зовнішніх, довільно заданих функцій. Кожна функція має бути ступенем свободи теорії, щоб її еволюція визначалася самоузгоджено через рівняння руху Лагранжа, які мають перший або другий порядок.
Можливо, що лагранжіан містить також похідні вищого порядку, ніж перший, але такі теорії сильно обмежені проблемою привидів, про яку ми згадаємо нижче, і тим фактом, що відповідні рівняння руху зазвичай описуються необмеженим гамільтоніаном, тобто система нестійка (теорема Остроградського [20,21]).
Наприклад, для гравітаційного лагранжіану в 4 вимірах ми можемо припустити тільки функцію, залежну від R та її похідних, де R - скаляр кривизни Рімана.
2.1.3 Лоренц-інваріантність
Ми також висуваємо вимогу лоренц-інваріантності теорії. Зверніть увагу, що ця вимога набагато сильніша, ніж вимога простої "коваріантності". У теорії не повинно бути жодних "абсолютних елементів", крім істинних констант.
Лоренц-коваріантність завжди може бути досягнута шляхом переписування рівнянь. Як приклад розглянемо лагранжіан, заданий у плоскому просторі формулою (∂ t φ) 2 - (∂ x φ) 2. ОН явно не є лоренц-інваріантним. Однак ми можемо тривіально записати цей член у коваріантній формі
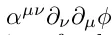 , задав
, задав 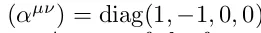 . Щось подібне, звісно, не повинно допускатися у фундаментальній теорії. Член у формі
. Щось подібне, звісно, не повинно допускатися у фундаментальній теорії. Член у формі 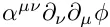
допустимий тільки в тому разі, якщо він сам є динамічним у полі теорії. Саме це ми маємо на увазі, вимагаючи, щоб теорія не містила "абсолютних елементів", тобто була лоренц-інваріантною, а не просто коваріантною.
2.1.4 Привиди
Привиди - це поля, кінетичний член яких має неправильний знак. Таке поле, замість того щоб сповільнюватися при підйомі потенціалу, прискорюється. Ця нестабільна ситуація призводить до серйозних проблем, коли ми хочемо квантувати його.
Загальновизнано, що така теорія не має сенсу, принаймні, на квантовому рівні. Це не дивно, оскільки квантування зазвичай розуміється як визначення збуджень над деяким основним станом, а теорія з привидом не має чітко визначеного основного стану. Його кінетична енергія припускає неправильний знак, і що більша φ̇ 2, то менша енергія.
2.1.5 Тахіони
Це ступені свободи, які мають від'ємну масу в квадраті, m2 < 0. Використовуючи знову приклад простого скалярного поля, виходить, що друга похідна потенціалу відносно "вакуумного значення" (φ = 0, з ∂ φ V (0) = 0) негативна, ∂ φ 2 V (0) < 0.
Не те, що теорія не має сенсу, скоріше, φ = 0 - поганий вибір для розширення, бо це максимум, а не мінімум потенціалу, тому й виникає нестійка рівновага.
Водночас теорія не може бути квантованою навколо класичного розв'язку φ = 0, але вона може стати хорошою квантовою теорією простим зсувом φ → φ - φ0, де φ0 - мінімум потенціалу. Якщо потенціал фундаментального скалярного поля не має мінімуму, а тільки максимум, то ситуація серйозніша. Тоді теорія дійсно нестійка.
Останні дві проблеми, разом із нестійкістю Остроградського, що з'являється в теоріях із вищими похідними, можна звести до такого: значуща теорія повинна мати обмежений функціонал енергії.
2.1.6 Надсвітлова швидкість і причинність
Фундаментальна фізична теорія, в якій дотримується інваріантність Лоренца, не допускає надсвітлових швидкостей. Якщо ця умова не виконується, ми можемо побудувати замкнуті криві, якими сигнал поширюється таким чином.
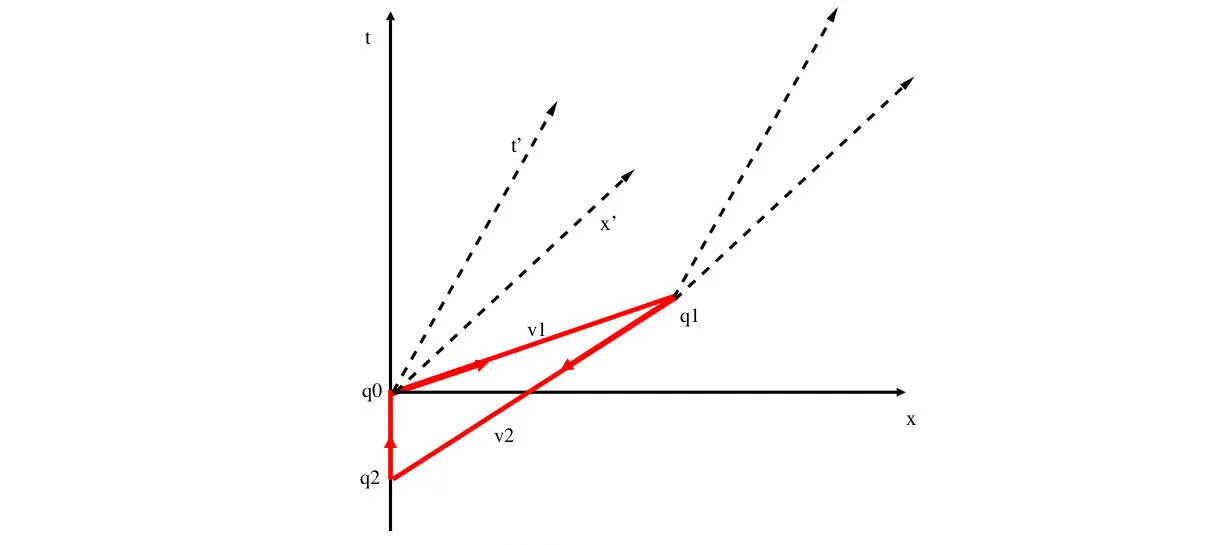
Розглянемо моди поля φ, які можуть поширюватися швидше за швидкість світла, зі швидкостями v 1 > 1 і v 2 > 1. Розглянемо систему відліку R і систему відліку R′, яка прискорена відносно R зі швидкістю v у напрямку x, і які збігаються на початку координат, q 0 (див. рис. 2).
Ми вибираємо v таким чином, що 1/v 1 < v < 1. Тепер спостерігач в R посилає сигнал із q0, координати якого дорівнюють
(t, x) = (0, 0) = (t′ , x′ ), зі швидкістю сигналу v 1 у напрямку x. У момент часу t1 цей сигнал приходить до події q1 , з координатами (t1 , x1 ) в R-кадрі, де x1 = v1t1 .
Там його приймає спостерігач, який перебуває у спокої відносно R′, і який повертає сигнал зі швидкістю v2′ у напрямку -x до події q2 = (t2,0) (див. рис. 2). Ми хочемо показати, що за відповідного вибору v2′ час t2 стає від'ємним.
Ми позначимо позиції та часи в прискореній рамці як R′. Тоді маємо x′2-x′1 =v2′(t′2-t′1 ). Застосовуючи звичайні формули для перетворень Лоренца, знаходимо, що 0=x2=γ(x′2+vt′2) і t2 =γ-1t′2 .
З іншого боку, ми маємо x′1=γ(x1-vt1)=γ(v1 - v)t1 і t′1 =γ(t1-vx1 )=γ(1-vv1)t 1 . Зауважимо, що оскільки ми вимагаємо, щоб vv1 >1, з цього випливає, що t′1 від'ємне.
Сигнал, який рухається зі швидкістю, більшою за 1/v у кадрі R, рухається в минуле в кадрі R′. Подія (t′1, x′1), за якої сигнал досяг позначки x′1, настає раніше, ніж подія (0, 0), коли він залишає позицію 0.
Щодо R ситуація протилежна: сигнал залишив 0 раніше, ніж досяг x1, t1 > 0. Те ж саме станеться, якщо ми тепер
надішлемо назад сигнал з 0 в R′ зі швидкістю |v2′| >1/v. Цей сигнал рухатиметься назад у часі t відносно R і прийде раніше, ніж у момент часу t1, коли його було надіслано.
Для досягнення ∆t′ =t′2-t′1 = γ(∆t - v∆x) = γ(1 - vv2 )∆t > 0, і водночас ∆t < 0, нам потрібно, щоб vv2 > 1, отже, v2 >1/v.
Як видно з рис. 2, v2 , яка є зворотною величиною нахилу прямої лінії, що з'єднує q2 і q1, має бути меншою за v1, зворотний нахил прямої від q0 до q1 . Отже, необхідно, щоб 1/v1<1/v2.
Петля, що утворилася таким чином, не є "причинною", оскільки і траєкторія від q0 до qi, і траєкторія від qi до q2 є просторовоподібними. Тому ми не можемо говорити про формування замкнутих причинних петель, але, тим не менш, це замкнена петля, якою може поширюватися сигнал і яка, отже, дає змогу побудувати машину часу, що призводить до звичайних проблем із причинністю та ентропією.
Добре відомо, що в теорії відносності події з просторовоподібним поділом, такі як q0 і qi або qi і q2 , не мають чітко визначеної хронології.
Залежно від системи відліку, одна з них відбувається раніше за іншу. Тому надсвітловий рух призводить до можливості існування машин часу.
Надсвітловий рух не сумісний з еквівалентністю всіх інерціальних систем відліку. Якщо ми допускаємо надсвітловий рух, але водночас вимагаємо, щоб сигнали надсилали тільки вперед у часі, то подія, наприклад, q2, що лежить у минулому qi в системі відліку R, може бути досягнута за допомогою сигналу, випущеного в системі відліку R', але її не можна досягти, якщо сигнал випускають із джерела в R.
У системі відліку, яка рухається зі швидкістю v = 1/vi відносно R, мода, що поширюється зі швидкістю vi в R, має нескінченну швидкість. Це означає, що рівняння поширення для цієї моди не має вигляду вже еліпса, тобто воно стало рівнянням обмежень.
У цій системі відліку еволюція моди в прямому світловому конусі малої плями більше не може бути визначена значеннями поля (і їхніх перших похідних) у малій плямі; рівняння моди нелокальне.
У всіх системах відліку, що рухаються зі швидкістю v>1/vi відносно R, існують два напрямки, в яких моди зі швидкістю поширення vi підкоряються еліптичним рівнянням руху. Отже, проблема Коші в цій логіці не є добре поставленою. Це зводить нанівець еквівалентність усіх систем відліку.
На перший погляд можна подумати, що лоренц-інваріантний лагранжіан автоматично забороняє надсвітлові рухи. Але ситуація не така проста. Уже в 1960-х роках Вело і Цванцигер [23] виявили, що загальні лоренц-інваріантні теорії з вищим спіном, s>1, призводять до надсвітлових рухів. Хоча рівняння явно лоренц-інваріантні, їхні характеристики в загальному випадку не збігаються зі світловим конусом і цілком можуть бути просторовоподібними. Із цього правила є винятки, серед яких теорія Янга-Міллса для спіна 1 і лінеаризовані рівняння Ейнштейна для спіна 2.
Можна заперечити на тій підставі, що загальна теорія відносності, яка, безумовно, є прийнятною (принаймні, на класичному рівні), може призвести до замкнутих причинно-наслідкових кривих, навіть якщо вона не допускає надсвітового руху.
У минулому було побудовано кілька рішень загальної теорії відносності із замкнутими причинними кривими, див., наприклад [24,25,26].
Але ці конструкції вимагають нескінченної енергії, як у роботі [25], з двома нескінченними енергіями [25] або двома нескінченно довгими прямими космічними струнами; отже, вони повинні порушувати умову домінантної енергії, як у роботі [24], де червоточини, як у роботі [25]. [24] або замкнута каузальна крива прихована за горизонтом подій, як у роботі [26], де звичайне замкнене коло в просторі перетворюється на каузальну криву шляхом переміщення його за горизонт, - тут відповідна кутова координата стає часовою.
Проте можливість замкнутих причинних кривих у загальній теорії відносності за певних умов залишається предметом занепокоєння, див., наприклад, [27].
Ситуація дещо інша, якщо надсвітловий рух можливий тільки у фоні, що порушує лоренц-інваріантність. Тоді виникає бажана рамка і можна вказати, що збурення завжди повинні поширюватися з функцією Гріна в цій рамці [28].
Проте слід визнати, що існують прискорені рамки, щодо яких задача Коші для надсвітлових мод не є добре визначеною. Фізика, яку відчуває спостерігач у такій рамці, дуже незвичайна (м'яко кажучи).
Властивості аналітичності мають багато інших важливих наслідків, як-от обмеження Фруассара, що передбачає, що повний переріз сходиться за високих енергій [29].
2.2 Ефективні теорії низьких енергій
Концепція низькоенергетичних ефективних теорій надзвичайно корисна у фізиці. Як один із найяскравіших прикладів розглянемо надпровідність. Це явище неможливо описати за допомогою повної квантової електродинаміки з типовою енергетичною шкалою в МеВ, в той час як енергетична шкала надпровідності становить міліеВ і менше.
Однак багато аспектів надпровідності можуть бути успішно описані за допомогою теорії Гінзбурга-Ландау комплексного скалярного поля.
Мікроскопічно це скалярне поле можна ототожнити з куперівською парою з двох електронів, але це не має значення для багатьох аспектів альтернативних теорій, зокрема, теорії струн.
Інший приклад - слабка взаємодія та теорія чотирьох Фермі. Остання є гарним наближенням до слабких взаємодій в енергетичних масштабах, набагато нижчих за масу Z-бозона.
Більшість фізиків також розглядають стандартну модель фізики частинок як низькоенергетичну ефективну теорію, що є справедливою нижче певного високоенергетичного масштабу, за яким стають актуальними нові ступені свободи.
Тепер ми хочемо дослідити, які з властивостей, описаних у попередньому підрозділі, можуть бути втрачені, якщо ми "інтегруємо" високоенергетичні збудження та розглядатимемо тільки процеси, що відбуваються за енергій, нижчих за певну шкалу відсічення.
Ми не можемо повністю ігнорувати всі частинки з масами вище, оскільки в низькоенергетичній квантовій теорії вони все ще можуть бути створені "віртуально", тобто за час менший, ніж 1/Ec. Це не має значення для початкового і кінцевого станів процесу розсіювання, але відіграє роль у взаємодії.
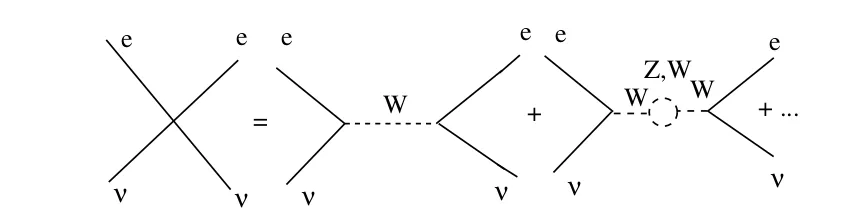
Як приклад розглянемо теорію 4-х Фермі. Вершина в 4 ферміонній взаємодії отримується інтегруванням за W і Z обмінами, як показано на рис. 3. Хоча кінцеві стани цієї теорії містять тільки електрони і нейтрино, віртуальна присутність масивних W і Z є життєво важливою для взаємодії між ними.
Повертаючись до нашого списку в попередньому підрозділі, ми, звичайно, хочемо зберегти перший пункт - математичний опис. Але формулювання лагранжіана також збережеться, якщо ми діятимемо послідовно, просто інтегруючи високоенергетичні ступені свободи.
А як щодо похідних вищого порядку в лагранжіані? Щоб відповісти на це запитання, давайте коротко повторимо основний аргумент теореми Остроградського для одновимірної частинки з залежним від часу положенням q(t).
Якщо лагранжіан залежить тільки від q і q̇, то вимога δS = 0 призводить до звичайного рівняння Ейлера-Лагранжа,

Тепер ми можемо ввести канонічні координати q і 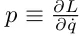 . Тоді гамільтоніан задається перетворенням Лежандра L за змінною q,
. Тоді гамільтоніан задається перетворенням Лежандра L за змінною q,

а рівняння Ейлера-Лагранжа тягне за собою канонічні рівняння

Ця процедура добре визначена, якщо лагранжіан недегенеративний, тобто якщо рівняння 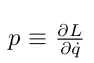 може бути розв'язком для q̇(q, p). Локально це еквівалент
може бути розв'язком для q̇(q, p). Локально це еквівалент 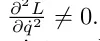 .
.
Ми припускаємо, що система автономна (немає зовнішньої залежності від часу). Тоді H = E є інтегралом руху, енергією розв'язку, і система називається стійкою, якщо H обмежена знизу. Якщо H не обмежена знизу, то взаємодії системи, наприклад, з випромінюванням, призведуть до величезного виробництва безмасових частинок, приводячи систему до дедалі нижчої енергії.
Якщо L залежить також від q, тобто L(q, q̇, q̈), то варіаційний принцип дає

Це диференціальне рівняння четвертого порядку, і його розв'язки залежать від чотирьох початкових даних, q(0), q̇(0), q̈(0) і q (0). Гамільтонове формулювання тепер потребуватиме чотирьох канонічних змінних, які можуть бути обрані як
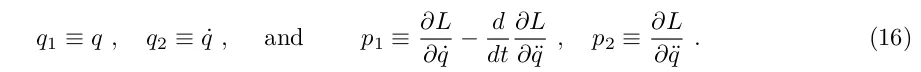
Гамільтоніан, отриманий перетворенням Лежандра лагранжіана відносно координат q̇ ≡ q 2 і q̈, дає
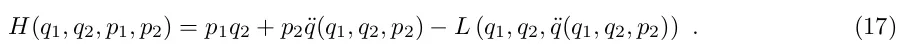
Цю процедуру добре визначено у q̈.а, якщо лагранжіан є недегенеративним у тому сенсі, що p 2 ≡ ∂L/∂ q̈ може бути інвертовано в детермінант q̈. Локально це проявляється як 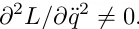
Легко перевірити, що канонічні рівняння сатисфікуються, а H є інтегралом руху. Але оскільки лагранжіан є функцією тільки трьох, а не чотирьох змінних, p1 не потрібен для вираження q̈ у термінах канонічних змінних. Він з'являється тільки лінійно в члені p1q2 і таким чином H не може бути обмежений знизу, тобто система нестійка.
Звісно, можна знайти добре керовані розв'язки цієї системи, оскільки для цього розв'язку енергія зберігається. Але щойно система почне взаємодіяти, наприклад, із гармонійним осцилятором, вона знижуватиме свою енергію і породжуватиме дедалі більше й більше коливальних мод.
Це особливо серйозно, якщо квантувати систему. Вакуум експоненціально нестійкий до одночасного виробництва мод позитивної та негативної енергії. Звісно, не можна просто "відсікти" рішення з негативною енергією, не порушуючи унітарності. І навіть якщо розглянута теорія, будучи лише низькоенергетичною ефективною теорією, вона має бути, принаймні, "унітарною за низької енергії".
Зрозуміло, що введення ще вищих похідних тільки погіршує ситуацію, оскільки ступінь рівняння Ейлера-Лагранжа збільшується на 2 з кожним новим ступенем свободи. Отже, якщо лагранжіан має ступінь 2 + n, то для опису гамільтоніану необхідне n +1 пар канонічних змінних, з яких тільки n + 2 необхідні для інверсії лагранжіану. Отже, n моментів з'являються тільки лінійно в членах p j q̇ j (q 1 , - - - - , q n + 1 , p n + 1 ), гамільтоніан має n нестійких напрямків.
У цій суперечці зовсім неважливо, чи є обговорювані нами ступені свободи фундаментальними або тільки низькоенергетичними ефективними ступенями свободи. Навіть якщо ми змінимо гамільтоніан при високих енергіях, нестійкість, яка є проблемою низької енергії, не зникне.
Є тільки два шляхи виходу з нестійкості Остроградського:
По-перше, якщо не виконується необхідна умова, щоб L була невиродженою.
Друга можливість - через обмеження.
У системі з m обмеженнями, у принципі, можна виключити m змінних. Отже, якщо система 2 + n порядку має n обмежень, то можна усунути всі нестійкі напрямки. На практиці це необхідно вивчати в кожному конкретному випадку.
Важливим прикладом для проблеми темної енергії є модифіковані гравітаційні лагранжіани виду
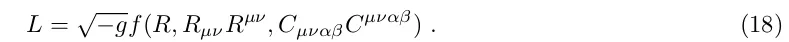
Тут R μν - тензор Річчі, C μναβ - тензор Вейля, а f (x1, x2, x3) - довільна функція, що не менше трьох диференціюється за часом. Оскільки тензори кривизни містять другі похідні від метрики, результуючі рівняння руху в загальному випадку будуть четвертого порядку, теорема Остроградського застосовна.
Звичайне гамільтонове формулювання загальної теорії відносності призводить до шести незалежних метричних компонентів g ij, які всі набувають вищих похідних.
Насправді існує тільки один вихід - випадок ∂ 2 f = ∂ 3 f = 0, тобто f може залежати тільки від R. Причина в тому, що в римановому скалярі R тільки одна компонента метрики містить другі похідні. У цьому разі новий ступінь свободи, що випливає, може бути повністю зафіксований обмеженням g 00, тож єдина нестійкість у теоріях f (R) - це звичайна нестійкість, пов'язана з гравітаційним колапсом (див. [21]).
Таким чином єдиними прийнятними узагальненнями загальної теорії відносності є теорії f (R), розглянуті в роботі [18].
Якщо теорема Остраградського не застосовна, у нас усе ще немає гарантій, що в теорії немає привидів або що потенційна енергія обмежена знизу (немає "серйозного" тахіона). Обмеження з теореми Остроградського, а також проблема привидів і тахіонів можуть бути сформульовані у вигляді вимоги, що теорія повинна мати функціонал енергії, обмежений знизу. Ця умова, звісно, не може зникнути в послідовній низькоенергетичній версії фундаментальної теорії, яка їй задовольняє.
Як і примари, нестійкість Остроградського в принципі може бути вилікувана додаванням члена ∝ (Φ/m)2 (∇φ)2 до нестійкого режиму φ, де φ - дуже важка частинка з масою M>>m, якою нехтували в низькоенергетичному наближенні теорії.
Однак це означає, що повна теорія низьких енергій фактично повинна містити член M/m) 2 (∇φ) 2. Висновкам, виведеним у рамках теорії низьких енергій зі зневагою до цього члена, у загальному випадку не можна довіряти. Тільки детальний аналіз кожного конкретного випадку може виявити, які результати теорії низьких енергій усе ще застосовні, а які змінені зв'язком із масивним полем φ.
Ба більше, відсічення високої енергії задаватиметься деяким масовим масштабом, тобто деяким лоренц-інваріантним енергетичним масштабом теорії, і тому ефективна теорія низьких енергій повинна також допускати лоренц-інваріантний лагранжіан. Лоренц-інваріантність не є високоенергетичним явищем, яке може бути просто втрачено при низьких енергіях.
Як щодо надсвітлового руху і причинності? Ми не хочемо вимагати певних властивостей матриці S до теорії низьких енергій, оскільки остання може не мати осмисленої пертурбативної квантової складової; як і теорія 4-х Фермі, вона перенормована.
Крім того, можна стверджувати, що в космології в нас є бажана рамка, тому лоренц-інваріантність порушується, і ми можемо просто вимагати, щоб усі надсвітлові моди поля поширювалися вперед у космічному часі. Тоді ніякі замкнуті сигнальні криві неможливі.
Але цей останній аргумент дуже небезпечний. Очевидно, що більшість розв'язків теорії лагранжіана дійсно мимовільно порушують більшість симетрій лагранжіана.
Але при застосуванні перетворення Лоренца ми отримуємо нове рішення, яке, з погляду лагранжіана, має таке ж право на існування.
Якщо деякі моди поля поширюються з надсвітловою швидкістю, це означає, що їхні характеристики просторовоподібні. Умова, що мода повинна рухатися вперед у часі щодо деякої рамки, має на увазі, що потрібно використовувати сповільнену функцію Гріна в цій рамці.
Оскільки просторовоподібні відстані не мають незалежної від рамки хронології, для просторовоподібних характеристик це твердження залежить від рамки. Залежно від системи відліку, дана мода може являти собою ступінь свободи, що нормально поширюється, або вона може задовольняти еліптичному рівнянню, обмеженню.
Ба більше, щоб переконатися, що режим поширюється вперед відносно однієї фіксованої системи відліку, доведеться використовувати іноді сповільнену, іноді випереджальну, а іноді похідну обох функцій, залежно від системи відліку.
У космологічній постановці це можна зробити послідовним чином, але далеко не зрозуміло, що такий припис може бути однозначно реалізовано для загальних низькоенергетичних рішень. Дійсно, у роботі [30] накидано рішення, яке не допускає цього, тож замкнуті криві сигналу знову можливі.
Тому ми вважаємо, що Лоренц-інваріантні низькоенергетичні ефективні лагранжіани, які допускають супер-люмінальне поширення певних мод, мають бути відкинуті. Проте цей випадок не настільки однозначний і в літературі існують протилежні думки, наприклад, [28].
З появою "ландшафту" [31] фізики почали розглядати антропні аргументи для обґрунтування своєї теорії, коли вона відповідає даним. Незважаючи на те, що існування життя на Землі є експериментальним фактом, ми вважаємо цей аргумент слабким, майже рівносильним відмові від фізики: "Речі такі, якими вони є, оскільки інакше нас би тут не було".
Тим не менш, ми вважаємо важливим поставити питання з суто теоретичного погляду, чи дійсно "все можливо" для ефективних теорій. У наступних розділах ми повернемося до основних вимог, які ми виклали в пройденій частині.
3 Загальні релятивістські підходи
Стандартна" загальна релятивістська інтерпретація темної енергії заснована на космологічній постійній як енергії вакууму:
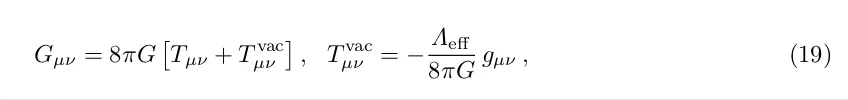
де тензор енергії-моментуму вакууму є лоренц-інваріантним. Цей підхід стикається з проблемою врахування неймовірно малого і дуже тонко налаштованого значення енергії вакууму, як узагальнено показано в рівнянні (8).
Теорія струн надає дражливу можливість у вигляді "ландшафту" вакуумів [31]. Очевидно, існує величезна кількість вакуумів, які допускає теорія струн, з широким діапазоном вакуумних енергій вище і нижче нуля. Це обговорюється у Буссо [15].
Ідея полягає в тому, що область Всесвіту, яку ми спостерігаємо, відповідає певній невеликій позитивній енергії вакууму, тоді як інші області з енергіями вакууму, що сильно відрізняються, виглядатимуть зовсім інакше. Безліч регіонів утворює в деякому сенсі "мультивсесвіт". Це цікава ідея, але вона вельми спекулятивна, і неясно, наскільки вона переживе подальший розвиток теорії струн у космології.
Альтернативним поглядом є інтерпретація A як класичної геометричної постійної (див., наприклад, [32]), нарівні з постійною Ньютона G. Таким чином, рівняння поля інтерпретуються геометрично,

За такого підходу невелике і тонко налаштоване значення Λ є не більшою загадкою, ніж безліч інших тонких налаштувань констант природи. Наприклад, зміна сили сильної взаємодії більш ніж на 2% означає, що не можуть утворюватися атоми, відмінні від водню, тому зірки та галактики не виникнуть.
Однак такий класичний підхід до Λ не позбавляє нас проблеми енергії вакууму - він просто переводить цю проблему в площину "чому вакуум не гравітує?".
Ідея полягає в тому, що фізика частинок і квантова гравітація якимось чином виявлять механізм скасування або симетрії, щоб пояснити, чому ρ vac = 0. Це було б простішим рішенням, ніж те, на яке вказує підхід струнного ландшафту, і дозволило б уникнути тривожних антропних аспектів цього підходу.
Проте не очевидно, чи є ця відмінність між Λ і ρ vac справді фізичним твердженням, чи чистою теорією, яка не може бути перевірена жодними експериментами.
У рамках загальної теорії відносності було досліджено різні альтернативи.
3.1 Динамічна темна енергія: квінтесенція
Тут ми замінюємо константу Λ/8πG на густину енергії скалярного поля φ, з лагранжіаном

так що в космологічних умовах,
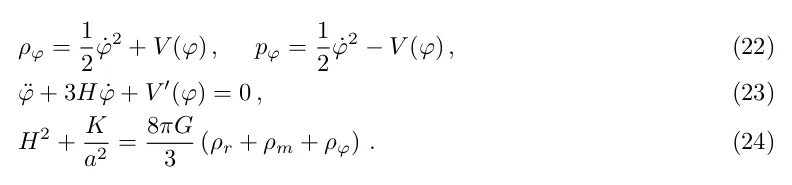
Поле сворачивает свой потенциал, и плотность темной энергии меняется на протяжении истории Вселенной. Были найдены "следящие" потенциалы, для которых плотность энергии поля следует за плотностью энергии доминирующего компонента материи. Это дает возможность решить или облегчить проблему тонкой настройки поля.
Хотя эти модели нечувствительны к начальным условиям, они требуют сильной тонкой настройки параметров лагранжиана, чтобы обеспечить недавнее доминирование поля, и, следовательно, не избавляют от проблемы совпадений. В более общем случае потенциал квинтэссенции, подобно потенциалу инфлатона, остается произвольным до тех пор, пока фундаментальная физика не выберет потенциал. В настоящее время не существует естественного выбора потенциала.
В заключение следует отметить, что пока нет убедительных причин для того, чтобы отдать предпочтение квинтэссенции перед моделью темной энергии LCDM. Модели квинтэссенции не кажутся более естественными, лучше мотивированными или менее надуманными, чем LCDM. Тем не менее, они являются жизнеспособной возможностью, а вычисления просты. Поэтому они остаются интересной мишенью для наблюдений. Более подробную информацию и ссылки можно найти в статье [16].
3.2 Динамическая темная энергия: более общие модели
Можно совместить квинтэссенцию с холодной темной материей, так что уравнения сохранения энергии становятся
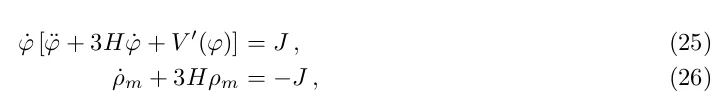
де J - обмін енергією [33,34].
Інша можливість - скалярне поле з нестандартним кінетичним членом у лагранжіані, наприклад,
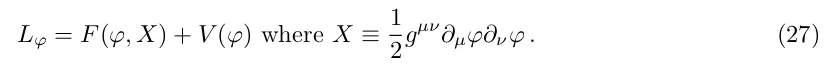
Стандартний лагранжіан має F (φ, X) = X. Деякі з нестандартних моделей F можуть бути виключені з теоретичних міркувань. Як приклад можна навести "фантомні" поля з від'ємною густиною кінетичної енергії (примари), F (φ, X) = -X. Вони мають w < -1, так що їхня густина енергії зростає з розширенням. Ця дивна поведінка відбивається в нестійкості квантового вакууму для фантомних полів.
Інший приклад - поля "k-есенції" [35], у яких F (φ, X) = φ -2 f (X). У цих теоріях немає привидів, і вони можуть виробляти прискорення в пізні часи. Швидкість звуку флуктуацій поля для лагранжіана в рівнянні (27) дорівнює

Для стандартного лагранжіана c 2 s = 1. Але для класу F, що породжують моделі прискореної k-есенції, виявляється, що завжди існує епоха, протягом якої c 2 s > 1, тож ці моделі можуть бути виключені відповідно до нашої вимоги причинності. Вони порушують стандартну причинність [36].
Для моделей, не виключених на теоретичних засадах, існує та сама загальна проблема, що і з квінтесенцією, тобто жодна модель не вмотивована краще, ніж LCDM, жодна не обрана фундаментальною фізикою, і будь-який вибір моделі більш-менш довільний. Квінтесенція, принаймні, має перевагу простоти - хоча LCDM має таку саму перевагу перед квінтесенцією.
Досліджуючи типові моделі темної енергії, ми завжди маємо пам'ятати, що оскільки і темна енергія, і темна матерія виявляються тільки гравітаційно, ми можемо виміряти тільки тензор повного імпульсу енергії темної компоненти(29)

Отже, якщо у нас немає інформації про рівняння стану темної енергії, існує виродження між рівнянням стану темної енергії w(t) і Ω dm. Без додаткових припущень ми не можемо виміряти жодне з них [37]. Це виродження стає ще гіршим, якщо ми допускаємо взаємодію між темною матерією і темною енергією.
3.3 Темна енергія як нелінійний ефект від структури
Оскільки формується структура і збурення густини матерії стає нелінійним, постають два запитання: (1) яким є ефект зворотної реакції цього нелінійного процесу на фонову космологію; (2) як нам провести коваріантне і калібрувально-інваріантне усереднення по неоднорідному Всесвіті, щоб отримати правильний FRW фон?
Спрощені відповіді на ці питання такі:
ефект нехтувано малий, оскільки він виникає на занадто малих масштабах, щоб бути космологічно значущим;
у світлі цього фон не залежить від формування структури, він такий самий, як і в лінійному режимі.
Для повного вирішення обох питань необхідний кількісний аналіз. Однак це дуже складно, оскільки істотно зачіпає нелінійні особливості загальної теорії відносності.
Були заяви, що ці спрощені відповіді хибні, і що, навпаки, ефекти досить великі, щоб імітувати Всесвіт, який прискорюється.
Дійсно, було драматичне і задовільне вирішення проблеми збігів, без необхідності будь-якого поля темної енергії. Звичайно, проблема того, чому вакуум не гравітує, залишається. Це питання обговорюється в роботі [17].
Однак зазначені міркування заперечуються, і справедливо сказати, що поки що немає переконливої демонстрації того, що прискорення може виникнути природним чином із нелінійних ефектів формування структури, див. [38]. Але тут слід зазначити, що ефекти зворотної дії/усереднення можуть бути значними, навіть якщо вони не призводять до прискорення.
Можливо також, що Всесвіт, який нас оточує, більше схожий на сферично симетричне, але неоднорідне рішення рівняння Ейнштейна - він більше схожий на Всесвіт Толмана-Бонді-Леметра, ніж на Всесвіт Фрідмана-Леметра.
Те, що здається нам космічним прискоренням, пояснюється в рамках простих моделей матерії, що містять тільки пил. Однак це означає, що ми перебуваємо дуже близько до центру величезної сферичної структури. Крім порушення принципу Коперника, виникає ще одна проблема тонкого налаштування. Ця ідея обговорюється в статті [4].
Прискорення в пізні часи від нелінійних ефектів формування структур - спроба в рамках загальної теорії відносності вирішити проблему збігів без поля темної енергії.
4. Модифікація теорії
Модифікований гравітаційний підхід поділяє припущення про відсутність поля темної енергії, але генерує прискорення за допомогою "темної гравітації", тобто ослаблення гравітації на найбільших масштабах, за рахунок модифікації самої загальної відносності.
Чи може прискорення Всесвіту в пізні часи бути гравітаційним ефектом? (Зауважимо, що це також не знімає проблему пояснення, чому енергія вакууму не гравітує).
Історичним прецедентом є спроби пояснити аномальну прецесію перигелію Меркурія "темною планетою", названою Вулканом. Зрештою, було виявлено, що необхідна модифікація ньютонівської гравітації.
Як ми стверджували в розділі 2, послідовна модифікація загальної теорії відносності вимагає коваріантного формулювання рівнянь поля в загальному випадку, тобто з урахуванням неоднорідностей і анізотропії. Недостатньо запропонувати спеціальні модифікації рівняння Фрідмана у вигляді
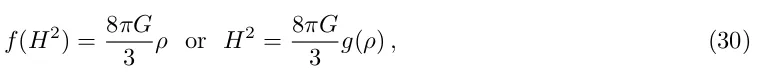
для деяких функцій f або g. Крім фундаментальних проблем, описаних у розділі 2, таке співвідношення дає нам змогу обчислити співвідношення відстані до наднової і червоного зміщення за допомогою цього рівняння. Але ми не можемо обчислити збурення густини, не знаючи коваріантної батьківської теорії, яка призводить до модифікованого рівняння Фрідмана. І ми також не можемо обчислити майбутнє Сонячної системи.
Дуже важко отримати інфрачервоні поправки до загальної теорії відносності, що задовольняють усім мінімальним вимогам:
- Теоретична узгодженість у сенсі, обговорюваному в розділі 2.
- Пізнє прискорення, узгоджене з даними щодо наднових.
- Час із переважанням матерії з еволюцією масштабного фактора А, яка узгоджується з вимогами формування структур.
- Збурення густини, які узгоджуються зі спостережуваним спектром потужності матерії, анізотропією МВФ і спектром потужності слабкого лінзування.
Стабільні статичні сферичні рішення для зірок і вакууму та узгодженість з обмеженнями спостережень на Землі та в Сонячній системі.
Узгодженість із даними про період бінарних пульсарів.
4.1 Скалярно-тензорні теорії
Загальна теорія відносності Ейнштейна має унікальний статус теорії, в якій гравітація опосередковується безмасовою частинкою зі спіном 2, а рівняння поля мають другий порядок. Якщо ми введемо модифікації дії Ейнштейна-Гільберта загального вигляду
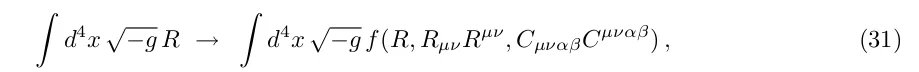
тоді рівняння поля стають рівняннями четвертого порядку, і гравітація переноситься також безмасовими полями спін-0 і спін-1. Щоб уникнути нестійкості Остроградського, про яку йшлося в розділі 2, ми накладаємо f = f (R), і вважаємо f "(R) = 0. Однак виявляється, що цьому спрощеному класу модифікованих теорій надзвичайно важко пройти спостережну й теоретичну перевірку. Прикладом може слугувати [39]

Для 
ця модель досягає прискорення в пізні часи, коли починає домінувати член μ/R. Однак модель страждає від нелінійних нестійкостей матерії та порушення обмежень Сонячної системи [40].
Для обходу цих проблем були введені варіації теорій f (R) [41]. Вони засновані на механізмі "хамелеона" для зміни модифікації загальної теорії відносності на межі між масивним тілом і зовнішнім вакуумом. Хоча такі механізми можуть бути успішними, моделі виглядають дедалі більш неприродними та надуманими - і страждають від дуже сильного тонкого налаштування.
Усі теорії f (R) приводять тільки до одного рівняння четвертого порядку [21]. Відповідний додатковий ступінь свободи може бути інтерпретований як скалярне поле, і в цьому сенсі теорії f (R) математично еквівалентні скалярно-тензорним теоріям через
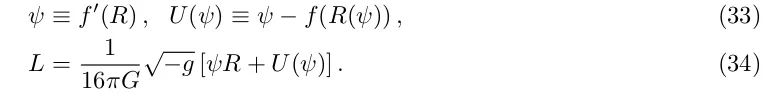
Цей лагранжіан може бути конформно перетворений у звичайну гравітацію зі скалярним полем, у модель квінтесенції, за допомогою перетворення (35)
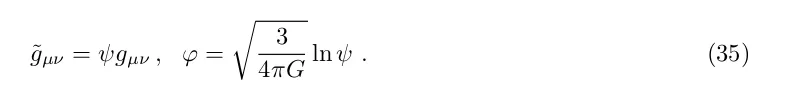
У термінах g̃ μν і φ лагранжіан стає стандартним лагранжіаном скалярного поля,
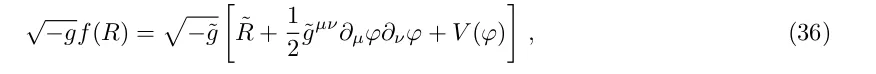
де
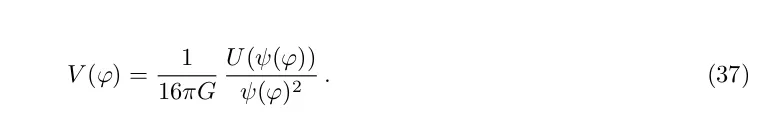
Цей приклад показує, що модифікацію гравітації (темна гравітація) або модифікацію тензора імпульсу енергії (темна енергія) можна розглядати як різні описи однієї й тієї самої фізики.
Тільки зв'язок скалярного поля φ зі звичайною матерією показує, що ця теорія походить від скалярно-тензорної теорії гравітації - і цей нестандартний зв'язок відображає той факт, що гравітація також опосередкована спін-0 ступенем свободи, на відміну від загальної відносності зі стандартним скалярним полем.
Більш загальні скалярно-тензорні теорії [42], які можуть бути мотивовані через
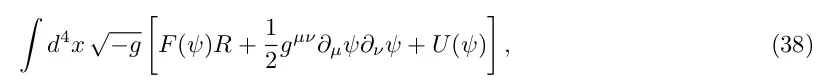
де ψ - поле зі спіном 0, що доповнює гравітон зі спіном 2.
У контексті прискорення пізнього часу ці моделі також відомі як "розширена квінтесенція". Скалярно-тензорні теорії містять дві функції, F і U. Ця додаткова свобода дає змогу гнучкіше підходити до спостережних і теоретичних обмежень.
Однак ціною за це є додаткова складність - теорії f (R) мають одну довільну функцію, а тут їх дві, F(0) і U(-0). Переважного вибору цих функцій із фундаментальної теорії не існує.
Загалом, модифікації дії Ейнштейна-Гільберта, що призводять до польових рівнянь четвертого порядку, або не задовольняють мінімальних вимог у найпростіших випадках, або містять більше складнощів і довільного вибору, ніж моделі квінтесенції в загальній відносності. Тому жодна з цих моделей не є серйозним конкурентом квінтесенції в загальній теорії відносності.
4.2 Моделі струнного світу
Тепер ми звернемося до класу моделей струнного світу, фон яких не складніший, ніж у LCDM, і які обіцяють стати серйозним суперником темної гравітації. Однак тут є приховані складнощі та проблеми, які ми пояснимо нижче.
Інфачервона модифікація загальної теорії відносності може виникнути в рамках квантової гравітації, на додачу до ультрафіолетової модифікації, яка має виникнути за високих енергій у дуже ранньому Всесвіті.
Судячи з усього, теорія струн здатна усунути нескінченності квантової теорії поля та об'єднати фундаментальні взаємодії, включно з гравітацією.
Але за це доводиться платити - теорія несуперечлива тільки в 9 вимірах простору.
Брани - це протяжні об'єкти вищої розмірності, ніж струни, і відіграють фундаментальну роль у теорії, особливо D-брани, на яких можуть закінчуватися відкриті струни.
Грубо кажучи, кінцеві точки відкритих струн, які описують частинки стандартної моделі, такі, як фермайони і калібрувальні бозони, прикріплені до бранів, тоді як закриті струни гравітаційного сектору можуть вільно переміщатися у більш високорозмірному "об'ємному" просторі-часі. Класично це реалізується через локалізацію матерії та полів випромінювання на брані, при цьому гравітація поширюється в об'ємному просторі (див. рис. 4).
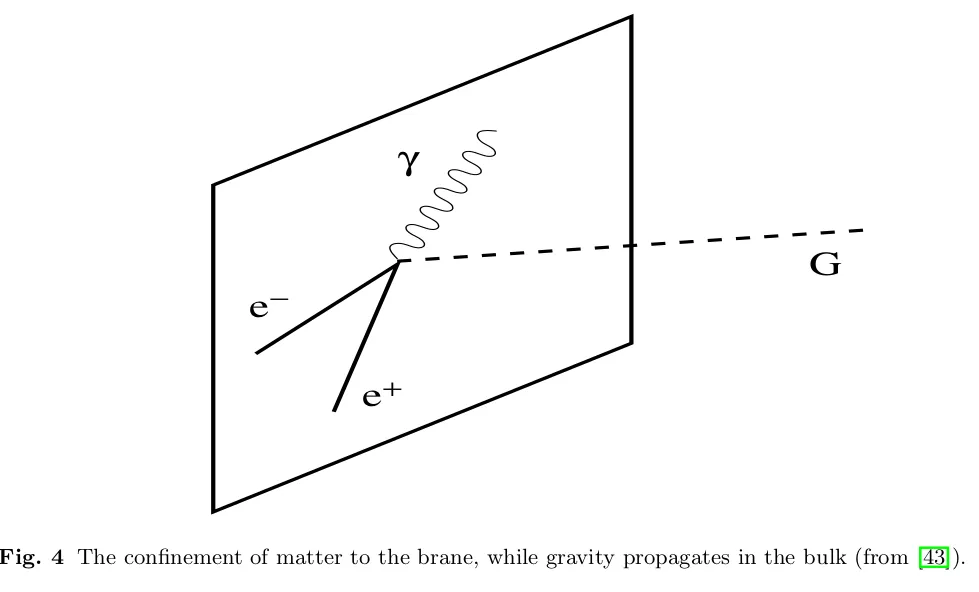
Реалізація теорії струн у космології надзвичайно важка з огляду на складність теорії. Це мотивує розвиток феноменології, як посередника між спостереженнями та фундаментальною теорією. (Дійсно, розвиток інфляційної космології був дуже цінною вправою у феноменології). Космологічні моделі струнного світу успадкували ключові аспекти теорії струн, але не намагаються нав'язати повний механізм теорії. Замість цього вводяться спрощення, щоб мати можливість побудувати космологічні моделі, які можна використовувати для обчислення спостережних прогнозів (огляди в цьому дусі див. у [44]).
Космологічні дані потім можуть бути використані для обмеження моделей струнного світу, а також як покажчики для подальшого розвитку теорії струн.
Виявляється, що навіть найпростіші моделі бранових світів напрочуд багаті - і обчислення їхніх космологічних збурень є складним і все ще неповним. Ключовою причиною цього є те, що гравітон вищої розмірності породжує вежу з чотиривимірних масивних спін-2 мод на брані, на додаток до стандартної безмасової спін-2 моди на брані (або, в деяких випадках, замість безмасової моди). У разі деяких моделей брани додатково існують як динамічні безмасові граві-скаляри і граві-вектори.
У більшості моделей бранових світів загальна відносність модифікується при високих енергіях. Основними прикладами є моделі типу Рендалла-Сундрума (РС) [47], де FRW-брана вбудована в анти-де-Сіттерівський об'єм із радіусом кривизни l.
За низьких енергій Hl ≪ 1, нульова мода гравітона домінує на брані, і загальна відносність відновлюється в хорошому наближенні.
За високих енергій, малих масштабів, Hl >> 1, масивні моди гравітона домінують над нульовою модою, і гравітація на брані поводиться дедалі п'ятовимірніше.
На брані діє стандартне рівняння збереження,(39)

але рівняння Фрідмана модифікується ультрафіолетовою поправкою:
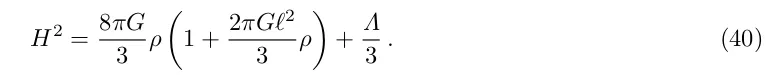
Член ρ 2 є ультрафіолетовою поправкою. За низьких енергій цей член нехтувано малий, і ми отримуємо H 2 ∝ ρ + Λ/8πG. За високих енергій гравітація "витікає" з брани, і H 2 ∝ ρ 2. Така поведінка 5D означає, що за заданої густини енергії швидкість розширення більша, ніж у загальній теорії відносності. Як наслідок, інфляція в ранньому Всесвіті змінюється цікавим чином [44].
Своєю чергою, модель подвійного світу Двалі-Габададзе-Порраті [45] (DGP), що була узагальнена на космологію Деффайє [46], змінює загальну відносність у пізні часи. Ця модель призводить до "самоприскорення" низькоенергетичного Всесвіту через ослаблення гравітації.
Як і модель RS, модель DGP є 5-мірною моделлю з нескінченним додатковим виміром. (Ми фактично припускаємо, що 5 додаткових вимірів у "батьківській" теорії струн можна ігнорувати за низьких енергій).
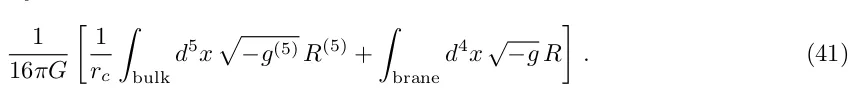
Припускається, що об'єм є п'ятовимірним простором Мінковського. На відміну від AdS-об'єму моделі RS, об'єм Мінковського має нескінченний об'єм. Отже, не існує нормалізованого нульового режиму (об'ємного) гравітона в брановому світі DGP.
Гравітація просочується з чотиривимірної брани в об'ємний світ на великих масштабах, λ > r c, де домінує перший член у сумі (41).
На малих масштабах гравітація ефективно пов'язана з браною, і чотиривимірна динаміка відновлюється з хорошим наближенням, оскільки домінує другий член. Перехід від 4- до 5-мірної поведінки регулюється масштабом переходу rc; гравітаційний потенціал слабкого поля поводиться як

Витік гравітації в пізніші часи ініціює прискорення - не через від'ємне поле тиску, а через ослаблення гравітації на брані. Чотиривимірна гравітація відновлюється за високих енергій через найлегші масивні моди п'ятовимірного гравітона, ефективно через надлегкий метастабільний гравітон.
Рівняння збереження енергії залишається таким самим, як і в загальній теорії відносності, але рівняння Фрідмана модифікується:

Інакше кажучи, у ранні часи, за Hr c ≫ 1, загальне релятивістське рівняння Фрідмана відновлюється. Навпаки, у пізні часи в МЧР-всесвіті, за умови 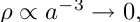 , маємо:
, маємо:

щоб розширення прискорювалося і було асимптотично де Ситтером. Оскільки H 0 > H ∞ , для досягнення самоприскорення в пізні часи нам необхідно:

і це підтверджується підгонкою спостережень наднових, як показано на рис. 5. Безрозмірний параметр перехресного переходу:

і відношення LCDM,

модифкований на:
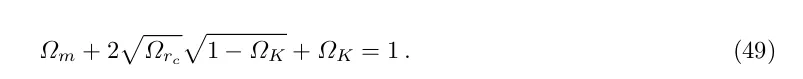
LCDM і DGP можуть пояснити спостереження наднових зі значеннями тонкого налаштування 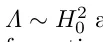 и
и 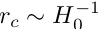
відповідно. Виродження може бути порушене спостереженнями, заснованими на утворенні структур, оскільки обидві моделі по-різному пригнічують ріст збурень густини [49].
Спостереження на основі відстаней спираються тільки на фонове чотиривимірне рівняння Фрідмана (44) у моделях DGP - і тому існують моделі квінтесенції в загальній відносності, які дають точно такі ж відстані до наднових, як і DGP [50].
Навпаки, спостереження за утворенням структур вимагають п'ятовимірних збурень у DGP, і не можна знайти еквівалентні моделі квінтесенції [51]. (Однак чотиривимірні моделі загальної відносності, що допускають анізотропні напруження, у принципі можуть імітувати DGP [53]).
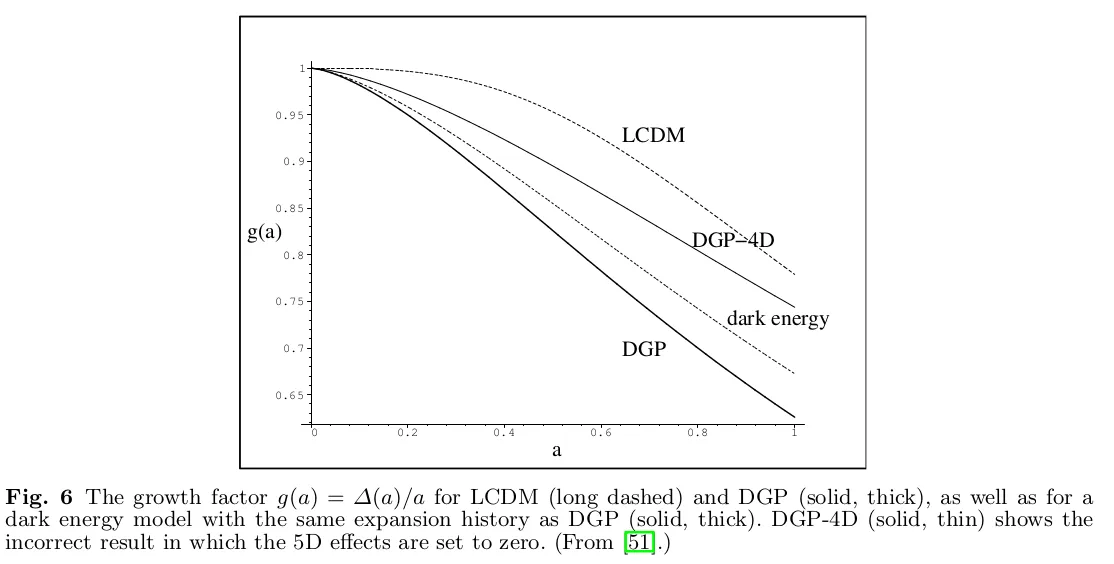
Для LCDM аналіз збурень густини добре вивчений. Для DGP він набагато тонший і складніший. Це обговорюється в роботі [19]. Хоча матерія обмежена чотиривимірною браною, гравітація в основі своїй п'ятовимірна, і об'ємне гравітаційне поле реагує на обурення густини і навпаки.
Еволюція збурень густини вимагає аналізу, заснованого на п'ятовимірній природі гравітації. Зокрема, п'ятовимірне гравітаційне поле створює анізотропну напругу в чотиривимірному Всесвіті. Якщо знехтувати цим напруженням і всіма 5D ефектами і просто розглядати збурення як 4D збурення з модифікованою фоновою швидкістю Габбла - то, як наслідок, порушується 4D тотожність Біанкі на брані, тобто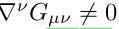
і результати виявляються суперечливими.
При включенні 5D ефектів [51,52] виконується 4D тотожність Біанкі. Узгоджене модифіковане рівняння еволюції для збурень густини на суббульбашкових масштабах має вигляд:
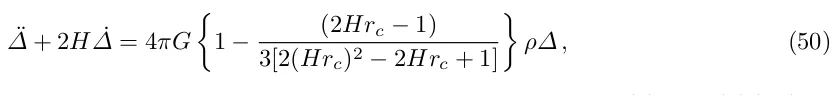
де член у дужках відображає поправку 5D. Лінійний коефіцієнт зростання, 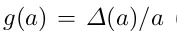 ,
,
показано на рис. 6.
На додаток до складності космологічних збурень, глибшу проблему створює той факт, що асимптотичне розв'язання де Ситтера в пізні часи в космологічних моделях DGP має привид [54].
Цей привид у гравітаційному секторі серйозніший, ніж привид у примарному скалярному полі. Фактично саме цей примарний ступінь свободи відповідальний за прискорення в моделі DGP. Проте вивчення DGP як іграшкової моделі темної гравітації може бути корисним.
5 Висновок
Докази прискорення Всесвіту в пізні часи продовжують зростати в міру збільшення кількості експериментів і якості даних - темна енергія або темна гравітація стають неминучою реальністю.
Це революційне відкриття, зроблене спостережною космологією, ставить теоретичну космологію перед серйозною кризою - як пояснити походження прискорення. Ядро цієї проблеми може бути "передано" фізиці частинок, оскільки на найфундаментальнішому рівні нам потрібне пояснення того, чому енергія вакууму або має неймовірно малу і тонко налаштовану величину, або дорівнює нулю. Обидва варіанти категорично не узгоджуються з наївними оцінками енергії вакууму.
Якщо прийняти, що енергія вакууму справді ненульова, то темна енергія описується Λ, то LCDM є найкращою з наявних моделей.
Космологічна модель потребує завершення через розвиток фізики частинок, яка пояснить значення енергії вакууму. У багатьох відношеннях, це найкраще, що ми можемо зробити в даний час, оскільки альтернативи LCDM, в рамках і за межами загальної відносності, не вирішують кризу енергії вакууму і, крім того, не мають переконливої теоретичної мотивації. Жоден із претендентів не виглядає краще, ніж LCDM.
Наразі, можливо, найпростішим і найпривабливішим претендентом є модель DGP з брановим світом. Однак простота рівняння Фрідмана оманлива, а складність її космологічних збурень включає проблему примарності.
На теоретичному рівні поки немає серйозного суперника для LCDM. Як і раніше, варто продовжувати досліджувати альтернативні моделі темної енергії і темної гравітації, щоб краще зрозуміти простір можливостей, різноманітність космологічних властивостей і наглядові стратегії, необхідні для їхнього розрізнення.
Водночас, у принципі, можливо, що космологічні спостереження, виявивши темну енергію/темну гравітацію, могли б виключити LCDM, показавши, з деяким прийнятним рівнем статистичної достовірності, що 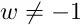 .
.
Зрештою, теоретична криза має не лише негативні наслідки: темна енергія/темна гравітація в космосі кидає захопливі виклики теорії та спостереженням.
Посилання
1. See, e.g., D. N. Spergel et al. [WMAP Collaboration], “Wilkinson Microwave Anisotropy Probe (WMAP) three year results: Implications for cosmology,”Astrophys. J. 657, 645 (2007) [arXiv:astro-ph/0603449]; W. J. Percival et al., “The shape of the SDSS DR5 galaxy power spectrum,” Astrophys. J. 665, 377 (2007) [arXiv:astro-ph/0608636].
2. S. H. Henry Tye, “Brane inflation: String theory viewed from the cosmos,” arXiv:hep-th/0610221; R. Kallosh, “On inflation in string theory,” arXiv:hep-th/0702059; A. Ashtekar, T. Pawlowski and P. Singh, “Quantum nature of the big bang: Improved dynamics,” Phys. Rev. D 74, 084003 (2006) [arXiv:gr-qc/0607039]; M. Bojowald, “Loop quantum cosmology,” Living Rev. Rel. 8, 11 (2005) [arXiv:gr-qc/0601085]; J. K. Erickson, S. Gratton, P. J. Steinhardt and N. Turok, “Cosmic perturbations through the cyclicages,” arXiv:hep-th/0607164; R. H. Brandenberger, “String gas cosmology and structure formation: A brief review,” arXiv:hep-th/0702001.
3. See, e.g., E. J. Copeland, M. Sami and S. Tsujikawa, “Dynamics of dark energy,” Int. J. Mod. Phys. D 15, 1753 (2006) [arXiv:hep-th/0603057]; L. Perivolaropoulos, “Accelerating universe: Observational status and theoretical implications,” arXiv:astro-ph/0601014;
S. Nojiri and S. D. Odintsov, “Introduction to modified gravity and gravitational alternative for dark energy,” Int. J. Geom. Meth. Math. Phys. 4, 115 (2007) [arXiv:hep-th/0601213]; T. Padmanabhan, “Dark Energy: Mystery of the Millennium,” AIP Conf. Proc. 861, 179 (2006) [arXiv:astro-ph/0603114]; N. Straumann, “Dark energy: Recent developments,” Mod. Phys. Lett. A 21, 1083 (2006) [arXiv:hep-ph/0604231]; S. Bludman, “Cosmological acceleration: Dark energy or modified gravity?,” arXiv:astro-ph/0605198; P. Uzan, “The acceleration of the universe and the physics behind it,” arXiv:astro-ph/0605313; D. Polarski, “Dark energy: Beyond general relativity?,” AIP Conf. Proc. 861, 1013 (2006) [arXiv:astro-ph/0605532]; R. Ruiz-Lapuente, “Dark energy, gravitation and supernovae,” Class. Quant. Grav. 24, R91 (2007)[arXiv:0704.1058].
4. K. Enqvist, this volume.
5. J. Goodman “Geocentrism reexamined”, Phys. Rev. D52, 1821 (1995) [arXiv:astro-ph/9506068].
6. G. F. R. Ellis and R. Maartens, “The emergent universe: Inflationary cosmology with no singularity,” Class. Quant. Grav. 21, 223 (2004) [arXiv:gr-qc/0211082].
7. R. Hlozek, M. Cortes, B. A. Bassett and C. Clarkson, this volume.
8. R. A. Knop et al. [The Supernova Cosmology Project Collaboration], “New Constraints on Ω M , Ω Λ , and w from an Independent Set of Eleven High-Redshift Supernovae Observed with HST,” Astrophys. J. 598, 102 (2003) [arXiv:astro-ph/0309368].
9. W. M. Wood-Vasey et al., “Observational Constraints on the Nature of the Dark Energy: First Cosmological Results from the ESSENCE Supernova Survey,” arXiv:astro-ph/0701041.
10. B. Leibundgut, this volume.
11. R. Nichol, this volume.
12. S. Sarkar, this volume.
13. G. Bressi, G. Carugno, R. Onofrio, and G. Ruoso, ”Measurement of the Casimir force between Parallel Metallic Surfaces”, Phys. Rev. Lett. 88, 041804 (2002); M. Bordag, U. Mohideen, and V. M. Mostepanenko, ”New Developments in the Casimir Effect”, Phys. Rept. 353, 1 (2001) [arXiv:quant-ph/0106045].
14. T. Padmanabhan, this volume
15. R. Bousso, this volume.
16. E. Linder, this volume.
17. T. Buchert, this volume.
18. S. Capozziello and M. Francaviglia, this volume.
19. K. Koyama, this volume.
20. M. Ostrogradski, Memoire Academie St. Petersbourg, Ser. VI 4, 385 (1850).
21. R. P. Woodard,“Avoiding Dark Energy with 1/R Modifications of Gravity” (2006) [arXiv:astro-ph/0601672].
22. C. Bonvin, C. Caprini and R. Durrer (2007) [arXiv:0706.1538].
23. G. Velo and D. Zwanzinger, “Propagation and Quantization of Rarita-Schwinger Waves in an External Electromagnetic Potential”, Phys. Rev. 186, 1337 (1969); G. Velo and D. Zwanzinger, “Noncausality and Other Defects of Interaction Lagrangians for Particles with Spin One and Higher”, Phys. Rev. 188, 2218 (1969).
24. M. S. Morris, K. S. Thorne and U. Yurtsever, “Wormholes, Time Machines and the Weak Energy Condition”, Phys. Rev. Lett. 61, 1446 (1988).
25. J. R. Gott, “Closed timelike curves produced by pairs of moving cosmic strings: Exact solutions”, Phys. Rev. Lett. 66, 1126 (1991).
26. A. Ori, “Formation of closed timelike curves in a composite vacuum/dust asymptotically-flat spacetime”, Phys. Rev. D76, 044002 (2007) [arXiv:gr-qc/0701024].
27. W. B. Bonnor B. R. Steadman, “Exact solutions of the Einstein-Maxwell equations with closed timelike curves”, Gen. Rel. Grav. 37, 1833 (2005).
28. E. Babichev, V. Mukhanov and A. Vikman, “k-essence, superluminal propagation, causality and emergent geometry” (2007) [arXiv:0708.0561].
29. M. Froissart, “Asymptotic Behavior and Subtractions in the Mandelstam Representation”, Phys. Rev. 123, 1053 (1961); For an overview see, C. Itzykson and J. B. Zuber, Quantum Field Theory, Chapter 5, McGraw Hill, New York (1980).
30. A. Adams, N. Arkani-Hamed, S. Dubovsky, A. Nicolis, and R. Rattazzi, “Causality, Analyticity and an IR Obstruction to UV Completion”, JHEP 0610, 014 (2006) [arXiv:hep-th/0602178].
31. J. Polchinski, “The cosmological constant and the string landscape,” arXiv:hep-th/0603249; R. Bousso, “Precision cosmology and the landscape,” arXiv:hep-th/0610211.
32. T. Padmanabhan, “Why does gravity ignore the vacuum energy?,” Int. J. Mod. Phys. D 15, 2029 (2006) [arXiv:gr-qc/0609012].
33. L. Amendola, G. C. Campos, R. Rosenfeld, “Consequences of dark matter-dark energy interaction on cosmological parameters derived from SNIa data” (2006) [arXiv:astro-ph/0610806].
34. Z.K. Guo, N. Ohta and S. Tsujikawa, “Probing the Coupling between Dark Components of the Universe”, Phys. Rev. D 76, 023508 (2007) [arXiv:astro-ph/0702015].
35. C. Armendariz-Picon, V. Mukhanov and P.J. Steinhardt, “Dynamical Solution to the Problem of a Small Cosmological Constant and Late-Time Cosmic Acceleration”, Phys. Rev. Lett. 85 4438 (2000) [arXiv:astro-ph/0004134 ].
36. C. Bonvin, C. Caprini and R. Durrer, “A no-go theorem for k-essence dark energy,” Phys. Rev. Lett. 97, 081303 (2006) [arXiv:astro-ph/0606584]; G. Ellis, R. Maartens and M. MacCallum, “Causality and the speed of sound,” arXiv:gr-qc/0703121.
37. M. Kunz, “The dark degeneracy: On the number and nature of dark components” (2007) [arXiv:astro-ph/0702615].
38. See, e.g.,E. W. Kolb, S. Matarrese, A. Notari and A. Riotto, “Primordial inflation explains why the universe is accelerating today,” arXiv:hep-th/0503117; G. Geshnizjani, D. J. H. Chung and N. Afshordi, “Do large-scale inhomogeneities explain away dark energy?,” Phys. Rev. D 72, 023517 (2005) [arXiv:astro-ph/0503553]; C. M. Hirata and U. Seljak, “Can superhorizon cosmological perturbations explain the acceleration of the universe?,” Phys. Rev. D 72, 083501 (2005) [arXiv:astro-ph/0503582]; E. E. Flanagan, “Can superhorizon perturbations drive the acceleration of the universe?,” Phys. Rev. D 71, 103521 (2005) [arXiv:hep-th/0503202]; S. Rasanen, “Backreaction and spatial curvature in a dust universe,” Class. Quant. Grav. 23, 1823 (2006) [arXiv:astro-ph/0504005]; A. A. Coley, N. Pelavas and R. M. Zalaletdinov, “Cosmological solutions in macroscopic gravity,” Phys. Rev. Lett. 95, 151102 (2005) [arXiv:gr-qc/0504115]; H. Alnes, M. Amarzguioui and O. Gron, “Can a dust dominated universe have accelerated expansion?,” JCAP 0701, 007 (2007) [arXiv:astro-ph/0506449]; M. Giovannini, “Gradient expansion(s) and dark energy,” JCAP 0509, 009 (2005) [arXiv:astro-ph/0506715]; Y. Nambu and M. Tanimoto, “Accelerating universe via spatial averaging,” arXiv:gr-qc/0507057; A. Ishibashi and R. M. Wald, “Can the acceleration of our universe be explained by the effects of21 inhomogeneities?,” Class. Quant. Grav. 23, 235 (2006) [arXiv:gr-qc/0509108]; T. Buchert, “On globally static and stationary cosmologies with or without a cosmological constant and the dark energy problem,” Class. Quant. Grav. 23, 817 (2006) [arXiv:grqc/0509124]; P. Martineau and R. Brandenberger, “Back-reaction: A cosmological panacea,” arXiv:astro-ph/0510523; R. Mansouri, “Illuminating the dark ages of the universe: The exact backreaction in the SFRW model and the acceleration of the universe,” arXiv:astro-ph/0601699; R. A. Vanderveld, E. E. Flanagan and I. Wasserman, “Mimicking Dark Energy with Lemaitre-Tolman-Bondi Models: Weak Central Singularities and Critical Points,” Phys. Rev. D 74, 023506 (2006) [arXiv:astro-ph/0602476]; J. W. Moffat, “Late-time inhomogeneity and the acceleration of the universe,” arXiv:astro-ph/0603777; A. Paranjape and T. P. Singh, “The Possibility of Cosmic Acceleration via Spatial Averaging in Lemaitre-Tolman-Bondi Models,” Class. Quant. Grav. 23, 6955 (2006) [arXiv:astro-ph/0605195].
39. S. Capozziello, S. Carloni and A. Troisi, “Quintessence without scalar fields,” arXiv:astro-ph/0303041.
40. See, e.g., L. Amendola, R. Gannouji, D. Polarski and S. Tsujikawa, “Conditions for the cosmological viability of f (R) dark energy models,” Phys. Rev. D75, 083504 (2007) [arXiv:gr-qc/0612180]; T. Chiba, T. L. Smith and A. L. Erickcek, “Solar System constraints to general f(R) gravity,” Phys. Rev. D75, 124014 (2007) [arXiv:astro-ph/0611867]; A. D. Dolgov and M. Kawasaki, “Can modified gravity explain accelerated cosmic expansion?,” Phys. Lett.B 573, 1 (2003) [arXiv:astro-ph/0307285].
41. W. Hu and I. Sawicki, “Models of f (R) Cosmic Acceleration that Evade Solar-System Tests” (2007) [arXiv:0705.1158v1]; A. A. Starobinsky, “Disappearing cosmological constant in f(R) gravity”, JETP Lett., 86, 157 (2007) [arXiv:0706.2041v2]. S. Nojiri and S.D. Odintsov, “Unifying inflation with LambdaCDM epoch in modified f(R) gravity consistent with Solar System tests”, Phys. Lett. B 657, 238 (2007) [arXiv:0707.1941]
42. B. Boisseau, G. Esposito-Farese, D. Polarski and A. A. Starobinsky, “Reconstruction of a scalar-tensor theory of gravity in an accelerating universe,” Phys. Rev. Lett. 85, 2236 (2000) [arXiv:gr-qc/0001066]; A. Riazuelo and J. P. Uzan, “Cosmological observations in scalar-tensor quintessence,” Phys. Rev. D 66, 023525 (2002) [arXiv:astro-ph/0107386]; G. Esposito-Farese, “Tests of scalar-tensor gravity,” AIP Conf. Proc. 736, 35 (2004) [arXiv:gr-qc/0409081]; S. Nesseris and L. Perivolaropoulos, “The limits of extended quintessence,” Phys. Rev. D 75, 023517 (2007) [arXiv:astro-ph/0611238].
43. M. Cavaglia, “Black hole and brane production in TeV gravity: A review,” Int. J. Mod. Phys. A 18, 1843
(2003) [arXiv:hep-ph/0210296].
44. R. Maartens, “Brane-world gravity,” Living Rev. Rel. 7, 7 (2004) [arXiv:gr-qc/0312059]; P. Brax, C. van de Bruck and A. C. Davis, “Brane world cosmology,” Rept. Prog. Phys. 67, 2183 (2004) [arXiv:hep-th/0404011]; V. Sahni, “Cosmological surprises from braneworld models of dark energy,” arXiv:astro-ph/0502032; R. Durrer, “Braneworlds,” AIP Conf. Proc. 782, 202 (2005) [arXiv:hep-th/0507006]; D. Langlois, “Is our universe brany?,” Prog. Theor. Phys. Suppl. 163, 258 (2006) [arXiv:hep-th/0509231]; A. Lue, “The phenomenology of Dvali-Gabadadze-Porrati cosmologies,” Phys. Rept. 423, 1 (2006) [arXiv:astro-ph/0510068]; D. Wands, “Brane-world cosmology,” arXiv:gr-qc/0601078.
45. G. R. Dvali, G. Gabadadze and M. Porrati, “Metastable gravitons and infinite volume extra dimensions,” Phys. Lett. B 484, 112 (2000) [arXiv:hep-th/0002190].
46. C. Deffayet, “Cosmology on a brane in Minkowski bulk,” Phys. Lett. B 502, 199 (2001) [arXiv:hep-th/0010186].
47. L. Randall and R. Sundrum, "An alternative to compactification," Phys. with cosmological constant," Phys. Lett. B 477, 285 (2000) [arXiv: hep-th/9910219].
48. R. Maartens and E. Majerotto, “Observational constraints on self-accelerating cosmology,” Phys. Rev. D 74, 023004 (2006) [arXiv: astroph/0603353].
49. A. Lue, R. Scoccimarro і GD Starkman, “Пробування Ньютону в значних масштабах: DGP тяжкості, космічної acceleration і великої сили структури,” Phys. Rev. D 69, 124015 (2004) [arXiv: astro-ph/0401515]; A. Lue and G. Starkman, “Gravitational leakage in extra dimensions: Здійснюючи значну енергію використання локальної тяжкості,” Phys. Rev. D 67, 064002 (2003) [arXiv: astro-ph/0212083].
50. EV Linder, “Cosmic growth history and expansion history,” Phys. Rev. D 72, 043529 (2005) [arXiv: astro-ph/0507263].
51. K. Koyama та R. Maartens, “Structure formation in the DGP cosmological model,” JCAP 0610, 016 (2006) [arXiv:astro-ph/0511634].
52. A. Cardoso, K. Koyama, SS Seahra і FP Silva, “Космологічні турботи в DGP braneworld: numeric solution”, arXiv:0711.2563.
53. M. Kunz та D. Sapone, “Dark Energy versus Modified Gravity”, Phys. Rev. Lett. 98, 121301 (2007) [aXiv: astro-ph/0612452].
54. D. Gorbunov, K. Koyama та S. Sibiryakov, “Більше на людях в DGP model,” Phys. Rev. D73, 044016 (2006) [arXiv: hep-th/0512097].