Перегляд квантової теорії через призму геометрії квантових станів розкриває перед нами нові перспективи для розуміння та управління фізичними властивостями матерії. Про це говориться в статті Physical Review Letters, яка була опублікована на цьому тижні.
Квантова теорія та інформація
Квантова фізика описує поведінку мікроскопічних систем, таких як атоми, молекули та електрони, за допомогою математичних абстракцій, наділених власними значеннями та станами. Власні значення визначають енергію та спін, тоді як власні стани детермінують ймовірності знаходження системи в певній конфігурації, задаючи положення або імпульс.
Традиційно основна увага квантової теорії приділялася власним значенням, оскільки вони піддаються безпосередньому вимірюванню і визначають результати експериментів. Однак останнім часом важливість власних станів стала більш очевидною, - ми хочемо більше знати про характер квантових систем, “технології” заплутаності й розраховувати топологію.
Ми також сподіваємось на заплутаність — фізичне явище, коли дві або більше квантових систем мають спільний квантовий стан і, таким чином, демонструють кореляції, що не можуть бути пояснені класичною фізикою.
Заплутаність визначає сутність квантової інформаційної науки і технології та спонукає використовувати квантову природу інформації для квантових обчислень і криптографії.
Своєю чергою, топологія дозволяє вивчати властивості форм, які зберігаються при безперервних деформаціях - розтягнення або скручування. Топологія дефінує структурні властивості власних станів, позначаючи симетрію та стійкість до збурень. Ми вже створили топологічні ізолятори та надпровідники, - і це тільки перші кроки в топологічних пошуках.
Автор статті стверджує, що заплутаність і топологія - лише два аспектами ширшої і потужнішої концепції, квантової геометрії. Мова йде про геометрію простору власних станів, тобто визначення детермінацій квантових станів від малих варіацій параметрів системи.
Таким чином, квантова геометрія описується додатковим математичним об'єктом, на зразок квантового геометричного тензора, що має дві складові: квантову метрику та кривину Беррі.
Квантова метрика вимірює відстань між квантовими станами і демонструє, наскільки вони ортогональні або перпендикулярні. Також вона впливає на локалізаційні властивості квантових станів, формуючи взаємодію у квантових системах.
Кривина Беррі вимірює кривизну простору квантових станів. Ми можемо прослідкувати фазові зміни незалежно від “розмірів”. В тому числі деякі ефекти, наприклад, ефект Холла та струм зсуву.
Еспериментальні спостереження
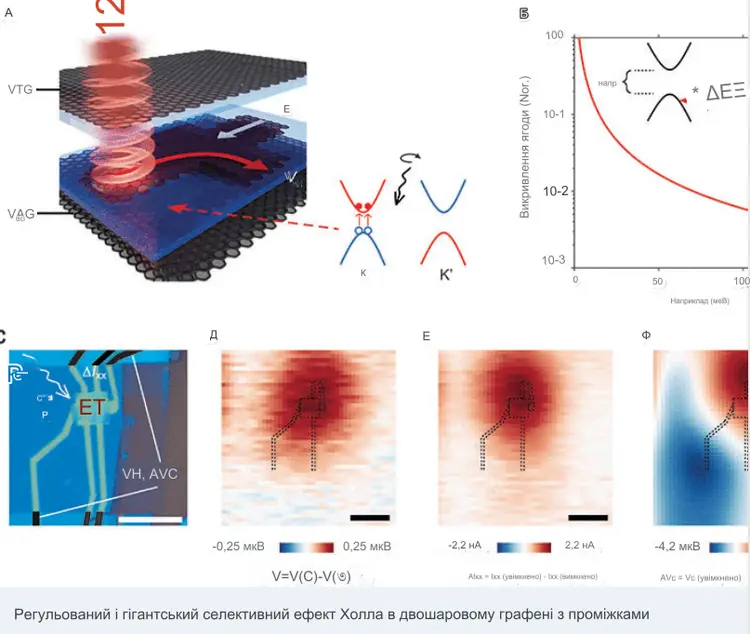
В статті детально аналізуються експериментальні спостереження ефектів квантової геометрії в різних фізичних системах, починаючи від вільних електронів у зонних ізоляторах і напівметалах і закінчуючи сильно корельованими електронами в дробових чернівських ізоляторах і плоскозонних надпровідниках.
В свою чергу, Барак Шошані, Університет Брока, Канада, таким чином пояснює, що таке квантова геометрія. Уявімо, що у нас є абстрактна квантова частинка. Ця система має деякі властивості, а ми записуємо квантовий стан системи як |ψ⟩
Це лише простий математичний спосіб записати вектор. Те, що позначено як |⟩, позначає “живий”, виміряний в конкретному вимірюванні квантовий стан нашої системи.
Квантові стани живуть у векторному або гільбертовому просторі. Тому ми допускаємо, що всі можливі стани системи є векторами в цьому просторі.
Далі, якщо у вас є деякі вектори у векторному просторі, ви завжди можете записати їх лінійною комбінацією. Наприклад, |A⟩+|B⟩ - в такому випадку це лінійна комбінація станів |A⟩ та |B⟩. Інакше кажучи, суперпозиція станів. В реальній природі її не існує, але фізикам потрібно якось її записати.
У квантовій механіці коефіцієнти кожного стану в суперпозиції називаються ймовірнісними амплітудами та позначаються комплексними числами (оскільки Гільбертів простір не що інше, як комплексний векторний простір).
Якщо ж ми вимірюємо суперпозицію, ми виміряємо тільки один зі станів в суперпозиції, з ймовірністю, що дорівнює квадрату абсолютної величини амплітуди.
Наприклад:
15−−√|A⟩+25−−√|B⟩+25−−√|C⟩
Тоді я виміряю A з ймовірністю 1/5, B з ймовірністю 2/5 або C з ймовірністю 2/5.
Тепер візьмемо більш складну систему, складену з двох окремих систем. Більший векторний простір.
Гільбертів простір задає квантовий стан так: |A⟩|B⟩, тобто частинка 1 знаходиться в стані |A⟩, частинка 2 - в стані |B⟩. Порядок має значення! Стан зліва або справа завжди є станом частинки 1 або 2 відповідно.
Отже, ми мали 1-частинкові стани, потім отримали суперпозиції їх, потім ми мали 2-частинкові стани. Наступний крок - суперпозиції 2-частинкових станів. І ось тут відбувається квантова заплутаність.
Уявімо, що є наступна суперпозиція:
12−−√|↑⟩|↑⟩+12−−√|↓⟩|↓⟩
Стрілки означають спін вгору |↑⟩ та спін вниз |↓⟩. Але стани можуть бути будь-якими, вони не повинні бути станами спіну.
Така суперпозиція означає, що якщо я вимірюю спін 2-частинкової системи, у мене є ймовірність 1/2 отримати |↑⟩|↑⟩ (тобто обидві частинки мають спін вгору) та ймовірність 1/2 отримати |↓⟩|↓⟩ (обидві частинки мають спін вниз). Квантова геометрія інтуїтивного зразка.
