У жовтні 2018 року Давид Асперо відпочивав в Італії, коли його осінило: є доказ розмірності нескінченності! Фундаментально нескінченність...
"Це був спалах осяяння", - пізніше згадував він.
Асперо, математик з Університету Східної Англії у Великій Британії, зателефонував Ральфу Шиндлеру з Університету Мюнстера в Німеччині, з яким він тривалий час співпрацював, і розповів про своє осяяння.
"Сказане було абсолютно незрозуміло для мене", - своєю чергою, розповідав Шиндлер. Але зрештою дует перетворив фантазію на тверду логіку.
Їхній доказ, опублікований у травні цього року в журналі Annals of Mathematics, об'єднує дві аксіоми, що конкурують, які були висунуті як основи для математики нескінченності. Асперо і Шиндлер показали, що одна з цих аксіом має на увазі іншу, що підвищує ймовірність того, що обидві аксіоми - вірні.
"Це фантастичний результат", - каже Менахем Магідор, математичний логік Єврейського університету в Єрусалимі. - Чесно кажучи, я й сам намагався його отримати".
"Це одна з найбільш інтелектуально захоплюючих, абсолютно драматичних речей в історії математики".
Нова теорія непрямим чином підтверджує аргументи проти гіпотези континууму, надзвичайно впливової гіпотези 1878 року про пласти нескінченностей. Обидві аксіоми, що зійшлися в новому доказі, вказують на хибність гіпотези континууму, а також на те, що додатковий розмір нескінченності знаходиться між нескінченно великими числами.
"Тепер у нас є послідовна альтернатива гіпотезі континууму", - упевнений Ільяс Фарах, математик із Йоркського університету в Торонто.
Цей результат - перемога для табору математиків, які в глибині душі відчувають, що гіпотеза континууму невірна.
Однак інший табір виступає за інше бачення математики нескінченності, тут гіпотеза континууму справедлива, битва між двома партіями ще далека від перемоги.
Нескінченність нескінченностей
Так, нескінченність буває різних розмірів. У 1873 році німецький математик Георг Кантор вразив науку до глибини душі, коли виявив, що "дійсні" числа, які заповнюють числову лінію - наприклад, 3,14159... - перевершують "натуральні" числа, такі як 1, 2 і 3, хоча і тих, і інших нескінченно багато.
Нескінченні набори чисел порушують нашу інтуїцію щодо розміру, тому як розминку порівняйте натуральні числа {1, 2, 3, ...} з непарними {1, 3, 5, ...}. Ви можете подумати, що перша множина більша, оскільки в другій множині трапляється тільки половина її елементів. Однак Кантор зрозумів, що елементи цих двох множин можна поставити у відповідність один до одного.
Перші елементи кожної множини (1 і 1) з'єднуються попарно, потім поелементно (2 і 3) і, нарешті, треті (3 і 5) і так далі до нескінченності, охоплюючи всі складові обох множин. У цьому сенсі дві нескінченні множини мають однаковий розмір, або те, що Кантор називав "кардинальністю". Він позначив їх кардинальним числом ℵ0 ("алеф-нуль").
Кантор також виявив, що натуральні числа не можуть бути поставлені у відповідність один до одного з континуумом дійсних чисел. Наприклад, спробуйте зіставити 1 з 1.00000... і 2 з 1.00001..., і ви пропустите нескінченно багато дійсних чисел (наприклад, 1.000000001...). Перерахувати їх усі неможливо: їхня кардинальність більша, ніж у натуральних чисел.
Але, на превеликий жаль Кантора, він не зміг цього довести.
У 1900 році математик Девід Гільберт поставив гіпотезу континууму на перше місце у своєму знаменитому списку 23 математичних проблем, які необхідно вирішити у 20 столітті. Гільберт був зачарований математикою нескінченності, що зароджувалася, - "канторівським раєм", як він її називав, - і гіпотеза континууму здавалася йому плодом, що висить низько.
Однак шокуючі відкриття минулого століття перетворили питання Кантора на глибоку епістемологічну загадку.
Проблема виникла 1931 року, коли народжений в Австрії логік Курт Гьодель виявив, що будь-який набір аксіом, який ви можете запропонувати як основу математики, неминуче буде неповним. Завжди є питання, які не вирішує список основних правил, а справжні математичні факти ніколи не можна довести.
Гьодель запідозрив, що гіпотеза континууму - це якраз той випадок: проблема, яка не залежить від стандартних аксіом математики.
Ці аксіоми, всього їх 10, відомі як ZFC (від "аксіоми Цермело-Френкеля з аксіомою вибору"), і вони лежать в основі майже всієї сучасної математики. Аксіоми описують основні властивості колекцій об'єктів, або множин. Оскільки практично все математичне випливає з множин (наприклад, порожня множина {} позначає 0; {{}} позначає 1; {{},{{}}} позначає 2 тощо), наявність правил достатня для побудови доказів у всій математиці.
У 1940 році Гьодель уточнив, що не можна використовувати аксіоми ZFC для спростування гіпотези континууму. Потім 1963 року американський математик Пол Коен ще більш посилив позицію - їх взагалі не можна використовувати для доказів. Тобто гіпотеза континууму не залежить від аксіом ZFC; вони можуть збігатися, а може й ні.
Крім гіпотези континууму, більшість інших питань про нескінченні множини також виявляються незалежними від ZFC. Така незалежність іноді трактується як щось, що не має відповіді, хоча більшість теоретиків вважають цю точку зору глибокою помилкою.
На їхню думку, у континууму є точний розмір; нам просто потрібні нові інструменти логіки, щоб зрозуміти, що це таке. Нові інструменти прийдуть у вигляді нових аксіом.
"Аксіоми не розв'язують проблеми", - каже Магідор, тому "ми маємо розширити їх до багатшої системи". Бракує саме ZFC як засобу досягнення математичної істини, а не самої істини.
З часів Коена теоретики множин мали намір зміцнити фундамент математики нескінченностей, намагаючись додати до списку ZFC додаткову аксіому. Вона має висвітлити структуру нескінченних множин, породити природні теореми, уникнути фатальних протиріч і, звісно, розв'язати питання Кантора.
Гьодель, зі свого боку, вважав, що гіпотеза континууму хибна - що існує більше чисел, ніж припускав Кантор. Він підозрював, що їх ℵ2. Він передбачав, як він писав 1947 року, "що роль проблеми континууму в теорії множин буде така, що вона врешті-решт призведе до відкриття нових аксіом, які дадуть змогу спростувати гіпотезу Кантора".
Джерело світла
Згодом з'явилися дві аксіоми-конкуренти, які начебто відрізнялися логічною несумісністю.
"Завжди існувала ця напруга", - каже Шиндлер.
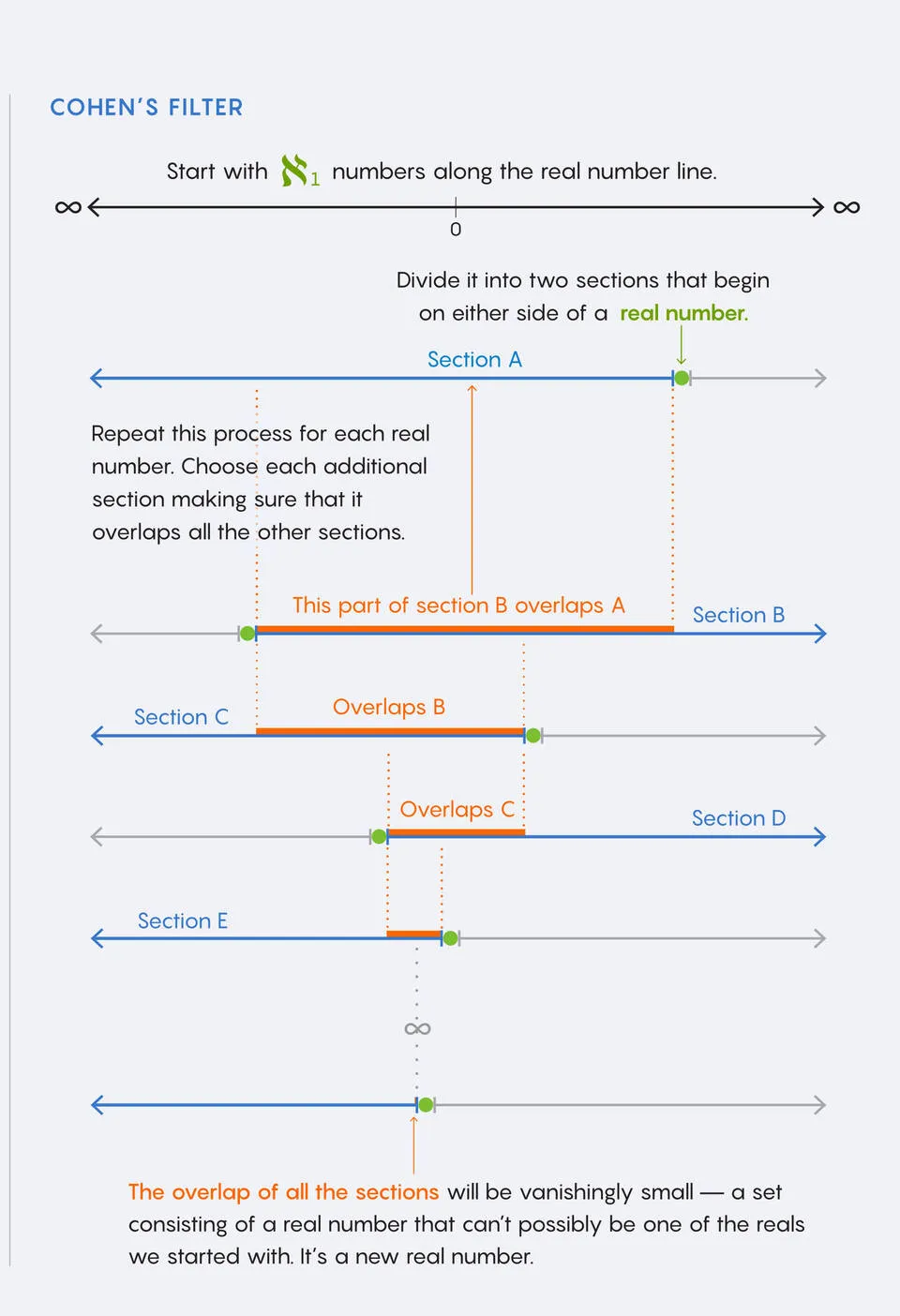
Щоб розібратися, ми маємо повернутися до роботи Пола Коена 1963 року, де він запропонував техніку форсування.
Почавши з моделі математичного всесвіту, яка містила ℵ1 ціле, Коен розширив континуум і включив у нього нове ціле за межами моделі. Математики незабаром виявили, що, залежно від специфіки процедури, форсування дає змогу додавати скільки завгодно чисел - ℵ2 або ℵ35, скажімо.
Крім нових дійсних чисел, математики узагальнили метод Коена, щоб придумати інші можливі об'єкти, однак деякі з них виявилися логічно несумісними один з одним. У результаті виник мультивсесвіт імовірнісних математичних всесвітів.
"Його метод створює двозначність у нашому всесвіті множин, - каже Г'ю Вудін, теоретик множин із Гарвардського університету. -Він створює хмару віртуальних всесвітів, і як я дізнаюся, в якому з них я перебуваю?".
Що було віртуальним, а що реальним? Який із двох конфліктуючих об'єктів, придуманих різними примусовими процедурами, має бути вирішений? Було неясно, коли і навіть чи існує об'єкт, тільки тому, що його можна уявити за допомогою методу Коена, насправді.
Щоб розв'язати цю проблему, математики висунули різні "аксіоми форсування" - правила, які встановлювали фактичне існування конкретних об'єктів, що стали можливими завдяки методу Коена.
"Якщо ви можете уявити, що об'єкт існує, значить, він існує; це і є керівний інтуїтивний принцип, який призводить до примусових аксіом", - пояснює Магідор. 1988 року він, Метью Форман і Сахарон Шелах довели постдекартівський принцип до логічного завершення, оголосивши максимум Мартіна, в якому йдеться про те, що все, що ви можете уявити собі за допомогою будь-якої процедури форсування, буде істинною математичною сутністю, якщо ця процедура задовольняє певній умові несуперечливості.
За всієї широти максимуму Мартіна, для того щоб одночасно розв'язати всі суперечності (задовольняючи водночас умову сталості), розмір континууму обмежили лише на консервативне ℵ2 - одне кардинальне число більше, ніж мінімально можливе значення.
Крім розв'язання проблеми континууму, максимум Мартіна виявився потужним інструментом для вивчення властивостей нескінченних множин. Прихильники цього стверджують, що він сприяє появі безлічі всеосяжних тверджень і загальних теорем. Навпаки, припущення, що континуум має кардинальність ℵ1, як правило, дає більше виняткових випадків і перешкод для доказів - "рай контрприкладів", за словами Магідора.
Максимум Мартіна став масово популярний як розширення ZFC. Але потім у 1990-х роках Вудін запропонував іншу аксіому, що вбиває гіпотезу континууму, але зовсім іншим шляхом. Вудін назвав цю аксіому (*), вимовляється як "зірка", тому що вона "схожа на яскраве джерело - джерело структури, джерело світла".
- (*) стосується моделі всесвіту множин, яка задовольняє дев'яти аксіомам ZF плюс аксіомі детермінованості, а не аксіомі вибору. Детермінованість і вибір логічно суперечать один одному, тому (*) і максимум Мартіна виявилися непримиренними. Але Вудін вигадав примусову процедуру, за допомогою якої можна розширити модель математичного всесвіту на більшу, яка узгоджується із ZFC, і саме в цьому всесвіті аксіома (*) правильна.
- "Що робить (*) такою цікавою, так це те, що вона дає змогу математикам стверджувати: "Для всіх X існує Y, таке, як Z", коли йдеться про властивості множин всередині однієї області. Такі твердження є потужним способом математичного міркування. Наприклад: "Для всіх множин ℵ1 речових, існують речові, які не входять до цих множин". Це заперечення гіпотези континууму. Таким чином, згідно з (*), гіпотеза Кантора хибна. Той факт, що (*) дозволяє математикам зробити цей висновок і стверджувати інші властивості множин дійсних чисел, робить її "привабливою гіпотезою", - міркує Шиндлер.
Маючи на руках дві високопродуктивні аксіоми, прихильники форсування зіткнулися з тривожним надлишком. "І аксіома форсування [максимум Мартіна], і аксіома (*) прекрасні й відчуваються п
Якби аксіоми суперечили одна одній, то прийняття однієї з них означало б пожертвувати іншою, тобто рішення могло б здатися довільним. "Вам довелося б вигадувати причини, чому одна з них є істинною, а інша хибною - або, можливо, обидві мають бути хибними", - каже Шиндлер.
Замість цього його нова робота з Асперо показує, що максимум Мартіна++ (технічна варіація максимуму Мартіна) передбачає (*).
Відсутня ланка
У молодості Асперо і Шиндлер працювали в одному з інститутів Відня. Одного разу Шиндлер прочитав рукопис, написаний, як зазвичай, від руки, теоретиком множин Рональдом Дженсеном.
У ньому Дженсен винайшов техніку, звану L-форсуванням. Шиндлера книга вразила, і він попросив свого студента спробувати розвинути цей метод. П'ять років потому, у 2011 році, він розповів про L-форсинг Асперо, який гостював у нього в Мюнстері. Асперо одразу ж припустив, що вони можуть можуть отримати (*) з максимуму Мартіна++.
У 2012 році математики оголосили, що у них є необхідний доказ. Вудін одразу ж виявив помилку, і дует відкликав статтю. У наступні роки вони часто поверталися до доказу, але незмінно виявлялося, що бракує однієї ключової ідеї - "відсутньої ланки", за словами Асперо, у логічному ланцюзі, що веде від максимуму Мартіна++ до (*).
Аналітичний план полягав у розробленні процедури форсування, подібної до L-форсування, за допомогою якої можна було б генерувати тип об'єкта, званий свідком. Цей об'єкт перевіряє всі твердження у формі (*). Доти, доки процедура примусу підкоряється необхідній умові несуперечливості, максимум Мартіна++ свідчить, що свідок, оскільки він може бути примушений до існування, існує. Таким чином, з цього випливає (*).
"Ми знали, як будувати такі примуси", - каже Асперо, але вони не могли зрозуміти, як гарантувати, що сама процедура примусу задовольнятиме ключову вимогу максимуму Мартіна. Досвід "спалаху", проведений Асперо на машині у 2018 році, нарешті, вказав шлях: необхідно розбити форсування на рекурсивну послідовність форсувань, кожне з яких задовольняє необхідним умовам.
Інші зірки
Збіжність максимуму Мартіна++ і (*) закладає міцний фундамент для вежі нескінченностей, де кардинальність континууму дорівнює ℵ2. "Питання в тому, чи правда це?" - запитує Пітер Келлнер, теоретик множин із Гарварду.
На думку Келлнера, знання того, що найсильніша аксіома примусу передбачає (*), може вважатися доказом як за, так і проти неї. "Насправді все залежить від того, як ви ставитеся до (*)", - шкодує математик.
Результат збіжності фокусує увагу на правдоподібності (*), оскільки (*) дає змогу математикам робити твердження на кшталт "для всіх X існує Y", які мають наслідки для властивостей дійсних чисел.
Незважаючи на надзвичайну корисність (*) у розв'язанні цих тверджень, здавалося б, без суперечностей, Келлнер належить до числа тих, хто має сумніви щодо аксіоми. Один з її наслідків - дзеркальне відображення структури певного великого класу множин набагато меншою множиною - здається йому дивним.
Примітно, що людина, яка була найбільш натхненна правоподібністю (*), зрештою налаштована проти неї. "Мене вважають зрадником", - стверджує Вудін.
25 років тому, коли виникло питання (*), він вважав гіпотезу континууму хибною, а отже, (*) - джерелом світла. Але близько десяти років тому несподівано змінив свою думку. Тепер він вважає, що континуум має кардинальність ℵ1 і що (*) і форсинг "приречені".
Вудін назвав доказ Асперо і Шиндлера "фантастичним результатом", який "заслуговує бути в "Анналах" - "Аннали математики" вважаються кращим математичним журналом - і визнав, що такий результат збіжності "зазвичай приймають як доказ якоїсь істини". Але він у неї не вірить. Є проблема, про яку згадав Кьолльнер, і ще більш серйозна проблема, яка виявилася завдяки власному досвіду 2019 року, незабаром після прочитання препринта статті Асперо і Шиндлера.
Вудін також поставив сильніші варіанти, звані (*)+ і (*)++, застосовні до повної потужної множини (множини всіх підмножин) дійсних чисел.
Відомо, що в різних моделях математичного всесвіту, якщо не в цілому, (*)+ суперечить максимуму Мартіна. У новому доказі, яким він почав ділитися з математиками в травні, Вудін показав, що (*)+ і (*)++ еквівалентні, а отже, (*)++ суперечить максимуму Мартіна в різних моделях.
(*)+ і (*)++ набагато перевершують (*) з однієї причини: вони дають змогу математикам робити твердження на кшталт "існує множина дійсних чисел..." і в такий спосіб описувати й аналізувати властивості будь-яких і всіх множин дійсних чисел. (*) не дає такої "екзистенціальної теорії" множин дійсних чисел. А оскільки максимум Мартіна, схоже, суперечить (*)+ і (*)++, здається, що екзистенціальні твердження про множини дійсних не можуть бути можливими в рамках максимуму Мартіна.
Для Вудіна це вирішальний фактор: "Це означає, що все приречене".
Інші основні учасники все ще перетравлюють доказ Вудіна. Але деякі з них підкреслили, що його аргументи мають можливий характер. Навіть Вудін визнає, що несподіване відкриття може змінити картину (і його думку), як це вже траплялося раніше.
Багато хто в співтоваристві очікує результатів спроби Вудіна довести гіпотезу "кінцевого L": тобто існування всеосяжного узагальнення модельного всесвіту множин Геделя.
Якщо скінченне L існує - а у Вудіна є всі підстави думати, що воно існує, і він уже на 400 сторінках намагається його довести - очевидно, що "аксіома мрії", яку треба додати до ZFC, має бути аксіомою скінченного L, або твердженням, що скінченне L - це всесвіт множин. І в граничному L Кантор правий: континуум має кардинальність ℵ1. Якщо доказ спрацює, то аксіома кінцевого L стане якщо не очевидним вибором розширення для ZFC, то, принаймні, грізним суперником максими Мартіна.
Відтоді, як Гьодель і Коен встановили незалежність гіпотези континууму від ZFC, математика нескінченності стала історією пригод, де теоретики множин можуть довести кількість чисел до будь-якого рівня - ℵ35, або ℵ1000, скажімо - і досліджувати наслідки.
Але оскільки результат Асперо і Шиндлера переконливо вказує на ℵ2, а Вудін наводить докази на користь ℵ1, встановилася чітка дихотомія, без абсолютного переможця. Більшість теоретиків множин хотіли б вийти з математичного мультивсесвіту й об'єднатися в картину канторівського раю, але заради чого заново вигадувати бога?
Низка вчених взагалі припускає, що ми повернемося в цей "долапсаріанський світ".
"Гільберт, коли виголошував свою промову, сказав, що людська гідність залежить від того, чи зможемо ми розв'язувати математичні задачі за принципом "так чи ні", - заявляє Джульєт Кеннеді, логічний математик і філософ з університету Гельсінкі. - Це було питання про спокуту людства, про те, чи є математика тим, чим ми завжди її вважали: встановленням істини. Не просто Ця Істина, а Та Істина. Не просто можливості. Ні. Континуум розмірений, і крапка".
Джерело: Quanta Magazine
