Здогадка професора Какея звучить як головоломка. Покладіть плазом голку на стіл. Яка потрібна площа для того, щоб повернути її так, щоб спрямувати її в усі можливі боки?
Найочевидніша відповідь - коло, діаметр якого дорівнює довжині голки. Але це не зовсім правильно. І за останнє століття зусилля математиків, які працювали в даному напрямі, показали: те, що здавалося кумедним питанням, насправді є глибоко провокаційною математичною проблемою про природу дійсних чисел - нескінченних прямих, що слугують координатами в просторі, де вперше було поставлено проблему.
Усе почалося з доказів, методологічно орієнтованих на розв'язання задачі про голку. Ці результати переносять вихідне питання з царини дійсних чисел, де математики опинилися в глухому куті, у геометричний і арифметичний світи, з їхніми альтернативними системами числення. Як виявилося, з ними легше працювати.
Винахідливість вдихнула в математиків нову душу.
"Припущення Какея здається важким, але водночас правдоподібно, що за кілька років буде знайдено рішення", - вважає Ларрі Гут, математик із Массачусетського технологічного інституту, який працює над цією проблемою понад 15 років.
Набір Какея
Сучасні версії гіпотези недалеко відійшли від початкового трактування, зробленого ще 1917 року. Японського математика цікавило питання про найменшу площу, необхідну в двовимірній площині, щоб повернути одновимірну лінію заданої довжини таким чином, щоб у підсумку вона вказувала на всі боки.
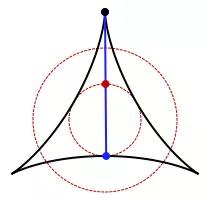
Для цього достатньо диска з діаметром, що дорівнює довжині лінії - просто обертайте лінію, як циферблат. Але можуть підійти й більш дрібні фігури.
Наприклад, візьмемо рівносторонній трикутник із висотою, що дорівнює довжині лінії. Виконавши низку поворотів, які, по суті, є триточковими, ви зміщуєте лінію - яка має нульову площу, оскільки вона одновимірна - навколо трикутника і додаєте бажану розмітку. Набір точок, який дає змогу виконати таке наведення, відомий як набір Какея.
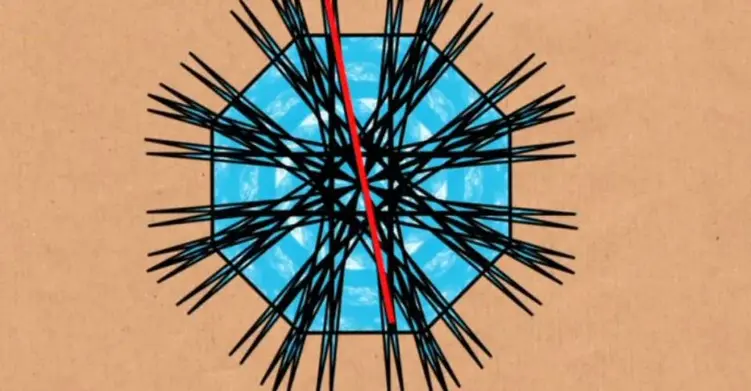
Японець хотів дізнатися найменш можливу площу множини. У 1919 році Абрам Бесікович дав дивовижну відповідь: немає межі тому, наскільки малим може бути набір Какея.
Він продемонстрував, що можна побудувати майже нескінченну кількість множин Какея, які доводять розміри рівностороннього трикутника до крайності. Замість трьох кутів трикутника виходить безліч кутів усередині кутів, що розходяться в усіх напрямках.
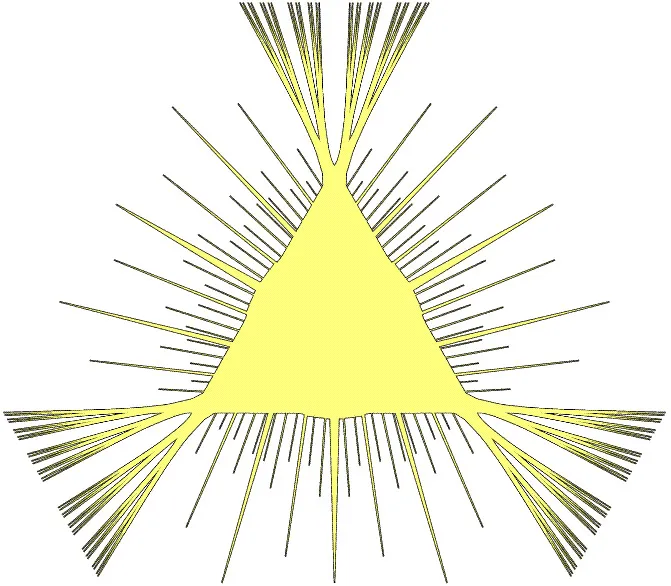
"У межі це дивна штука, схожа на їжака", - каже Зеєв Двір, професор Принстонського університету й автор одного з нових доказів. - У результаті виходить складна фрактальна структура з довільно малою площею, на стільки, що рівносильно відсутності площі взагалі".
Здавалося, побудова Бешиковича вирішила проблему. Але десятиліття потому математики розробили іншу версію, яка виявилася набагато неприємнішою.
Множини Какея і порожнеча
Бешикович довів, що множини Какея можуть мати площу, що зникає, але для опису розміру фігури є інші способи, крім площі. Такі множини, як і раніше, містять точки, але в 1970-х роках виникло інше питання: наскільки ефективно розташовані ці точки?
Це питання, що отримало назву "припущення Какея", пророкує, що якщо у вас є, скажімо, маленькі квадрати тканини, і ви намагаєтеся розташувати їх на наборі Какея так, щоб квадрати повністю покривали множину, то в якомусь дуже точному сенсі вам знадобиться багато квадратів для повного покриття.
Ступінь, у якій точки множини розташовані таким чином, що їх легше або важче покрити, відображається у двох тісно пов'язаних метриках, які називаються розмірністю Хаусдорфа і розмірністю Мінковського. Ці розмірності дають ще одну сувору основу для вивчення множин Какея.
Гіпотеза Какея передбачає, що розмірності Хаусдорфа і Мінковського множини Какея мають бути якомога більшими. Хоча точні визначення самих розмірностей є технічним питанням, інтуїція, що лежить в основі гіпотези, досить проста: щоб лінії проходили скрізь, потрібно багато чогось.
"У вас є по одній лінії в кожному напрямку, і уявіть, що ви намагаєтеся стиснути їх усі у щось. Як це можна стиснути?" - пояснює Гут.
Загадка Какея
Загадка Какея існує в евклідовому просторі, де точки визначаються дійсними числами - числами, які можуть мати нескінченно довгий десятковий дріб, наприклад 19,1777... або пі. Згодом стало зрозуміло, що речовинні координати є важливою частиною того, чому загадку Какея так важко розв'язати.
Що саме в дійсних числах створює перешкоду, не зовсім зрозуміло, але деякі особливості виділяються.
- По-перше, дійсні числа безперервні, що означає, що їх не можна розглядати на будь-якому дискретному інтервалі без втрати можливості виконувати арифметичні дії. Наприклад, якщо ви обмежите себе інтервалом між 1 і 2, ви втратите додавання.
- По-друге, дійсні числа нескінченні, тобто незалежно від того, наскільки сильно ви збільшуєте їхній масштаб, ви бачите одне й те саме в будь-якому масштабі.
- По-третє, речовинні числа можуть бути дуже близькі до нуля, не будучи насправді нулем.
"У цьому і полягає технічна складність", - вважає Джошуа Зал з Університету Британської Колумбії.
Складність дійсних чисел спонукала математиків розглянути версії гіпотези Какея, які задаються в менших системах числення. Наприклад, у них можуть бути тільки цілі числа від 1 до 5. І хоча ці системи числення не дуже схожі на дійсні числа, вони володіють багатьма з основних арифметичних властивостей і дають змогу виконувати додавання, віднімання, множення і ділення.
Вони також досить багаті, щоб підтримувати методи лінійної алгебри для визначення ліній, а коли у вас є лінії, ви можете поставити трохи змінену версію гіпотези Какея: яким є мінімальний розмір набору точок в одній із систем числення, коли можна побудувати лінію в будь-якому напрямку? Це запитання Томас Вольф поставив 1996 року. Відтоді математики підходять до нього як до будівельних риштувань, які наближають їх до відповіді на саму гіпотезу Какея.
"Ідея в тому, що проблема, ймовірно, простіша, і, можливо, слід спробувати розробити методи її розв'язання, щоб отримати ідеї для розв'язання справжнього евклідового випадку", - каже Манік Дхар із Прінстона, автор двох недавніх робіт, присвячених гіпотезі Какея.
Ілюзорне розв'язання задачі Какея
Щоб визначити одну із заданих невеликих систем чисел, спочатку потрібно вибрати число. Можливо, ви виберете 9, і тоді ваша система чисел міститиме цілі числа від 1 до 9. А можливо, ви виберете 17, 25 або 83.
Ваш вибір має значення. Зокрема, те, чи є це число (зване модулем) простим або непростим, і яким чином воно не є простим, чинить великий вплив як на поведінку системи числення, так і на методи, що застосовні для розв'язання задачі Какея.
У 2008 році Двір подолав задачу Какея для скінченних простих чисел, що є окремим випадком, який мав на увазі Вольф у 1996 році. Розв'язок відноситься до системи скінченних полів.
Двір довів, що в скінченних полях множина Какея обов'язково має найбільшу можливу розмірність (де розмірність переформульована таким чином, що набуває сенсу в скінченній системі). Його доказ, що складається всього з двох сторінок, значною мірою спирався на той факт, що коли модуль є простим, будь-яка множина в системі скінченних чисел слугує коренем поліноміального рівняння. Це означає, що множина може бути описана рівнянням так, як не описуються множини Какея в дійсних числах.
Доказ Двіра - перший серйозний прогрес у розв'язанні задачі Какея. На мить математики сподівалися на те, що евклідова задача Какея буде вирішена.
Але не так сталося, як передбачалося.
"Люди були дуже схвильовані, ми всі дуже старалися, але нічого не вийшло", - журиться Гут.
Системи числення не мають значення
У листопаді 2020 року Двір і Дхар, його аспірант, розв'язали задачу Какея для скінченних систем числення, де модулем є будь-яке число, точніше, добуток різних простих чисел, наприклад 15 (3 × 5). Ці системи чисел вимагали вийти за рамки поліноміального методу. Тому вони перетворили завдання на питання про матриці.
Тут стовпці представляють точки, а рядки - напрямки. Якщо в певній точці є лінія, що йде в певному напрямку, запишіть 1 у відповідному місці матриці. В іншому разі введіть 0.
Таким чином, матриця кодує властивості набору ліній. Тепер обчисліть властивості самої матриці та визначте властивості набору. Зокрема, "ранг" матриці безпосередньо пов'язаний із розміром набору ліній.
Дхар і Двір довели, що множина прямих велика, а отже, для конкретних систем числення гіпотеза Какея правильна - будь-яка множина точок, яка містить прямі в усіх напрямках, має бути великою.
Менш ніж за рік після отримання результату Дхара і Двіра Бодан Арсовскі вніс деякі уточнення. У серпні 2021 року він довів гіпотезу Какея для скінченних систем числення, у яких модулем виступає просте число, піднесене до степеня, наприклад, 9 (32). Із цього випливає гіпотеза нескінченної системи чисел, так званої р-адики.
Після виходу статті Арсовського математики кинулися з'ясовувати, чи можна модифікувати його методи, щоб застосувати їх до дійсних чисел. Через кілька місяців безплідних зусиль стало очевидно, що, принаймні, на даний момент це неможливо робити.
"Є невеликі відмінності в поведінці поля дійсних чисел і p-адичних полів, через які аналогія нібито руйнується", - пояснює Алехо Сальваторе, докторант Вісконсинського університету в Медісоні.
Далі відбулися ще два сюжетні повороти. У жовтні минулого року Дхар довів, що гіпотеза Какея правильна для скінченних систем чисел із будь-яким модулем. Потім у лютому Сальваторе підтвердив цю гіпотезу для більш екзотичних систем чисел, званих локальними полями позитивної характеристики, у яких кінцеве поле доповнюється змінною.
Можна по-різному ставитися до цього шквалу результатів. Один із них - сподіватися, що імпульс збережеться: тепер, коли математики доводять істинність гіпотези для окремих систем числення, можливо, наступними будуть дійсні числа.
Але є й інший варіант - зробити крок назад і запитати: чому математики досі не змогли підтвердити гіпотезу Какея для дійсних чисел з огляду на те, що вони змогли підтвердити її для інших систем?
Принаймні один математик вважає, що пояснення може бути найочевиднішим з усіх.
"Я більше не впевнений, що гіпотеза Какея правильна", - вважає Гут.
За матеріалами Quanta Magazine
