Якщо гравітація не є силою, чому ми шукаємо квантову теорію гравітації або гравітон?
Як відповідь на це запитання дозвольте мені, - каже Віктор Тот, астрофізик з університету Торонто, - спочатку навести цитату з маленької книжки, написаної однією людиною, яка вважала, що розуміє сенс теорії відносності. Зокрема:
"Ми [...] припускаємо [...], що рух матеріальної частинки, яка перебуває під дією тільки інерції та гравітації, описується рівнянням, яке описується рівнянням. Інші дослідники, які працюють із макроскопічними барабанами в стані квантової заплутаності, показали, як можна виміряти імпульс двох барабанних головок одночасно.
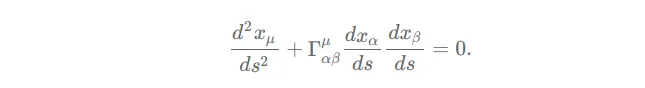
Фактично, це рівняння зводиться до рівняння прямої лінії, якщо всі компоненти гравітаційного поля, Γμαβ, зникають. [...] Рівняння виражають вплив інерції та гравітації на матеріальну частинку. [...] За аналогією з рівняннями Ньютона перший член можна розглядати як вираз для інерції, а другий - як вираз для гравітаційної сили".
Подумати тільки! Він вважав, що гравітація - це сила, тоді як усі знають, що це не сила, а просто геометрія!
Цей же горе-фізик в одному зі своїх листів так охарактеризував геометризацію гравітації: "Помилково думати, що "геометризація" - це щось суттєве. Це лише свого роду милиця для знаходження числових законів. Чи пов'язувати "геометричні" інтуїції з теорією - це... особиста справа кожного".
Ви можете задатися питанням, хто міг написати таку нісенітницю? Згідно з титульним аркушем вищезгаданої книги, авторство висловлювань належить Альберту Ейнштейну, творцеві загальної теорії відносності.
Інший фізик усе життя розважав студентів жартівливими міркуваннями, які він претензійно називав "Лекціями про гравітацію".
І дійшов до того, що розглядав гравітацію як силове поле, без будь-якої геометризації. Але зрештою написав фантастичний твір про венеріанських учених, які намагаються вирішити, яке силове поле краще - скалярне, спінорне, векторне чи тензорне.
Правильно зробив, бо зрештою він відновив рівняння поля Ейнштейна. Звали цього лектора Р. Фейнман.
Що ж до того, чому ми шукаємо квантову теорію гравітації, то, можливо, ці дві видатні особистості мали рацію. Одночасно.
Тільки подумайте про рівняння, яке вигадав перший із них,
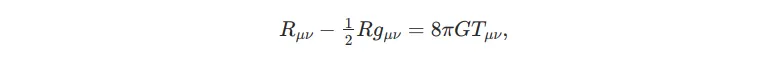
де ліва частина являє собою гравітацію, а права характеризує матерію.
Тепер ми знаємо, що матерія добре описується квантовою теорією, тому так званий тензор енергії-момента представлений не числами, а квантово-механічними операторами. Приблизно так:
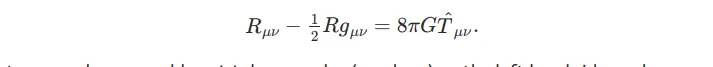
Але тоді в нас виникає проблема. Є яблука (числа) з лівого боку й апельсини (квантово-механічні оператори) з правого боку. Обидві сторони можуть бути рівними тільки в тому разі, якщо тотожні нулю. Що в принципі неможливо.
Одне з можливих рішень - замінити праву частину його середнім значенням, так званим значенням очікування:
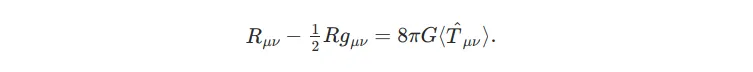
Це рішення, зване напівкласичною гравітацією, насправді працює напрочуд добре, але воно вважається досить неелегантним, ситуативним. Було б набагато краще, якби ми могли квантувати гравітацію.
Однак ми не знаємо, як квантувати гравітацію. Але ми знаємо, що незалежно від того, як ми будемо це робити, у слабкій, так званій "пертурбативній" межі вона може бути описана простими квантами, які ми називаємо гравітонами.
Що також вірно незалежно від конкретних деталей ще не відкритої квантової теорії гравітації. Це також означає, що якщо ми коли-небудь знайдемо експериментальні докази існування гравітонів, ми знатимемо, що гравітація має бути квантуваною, тому що напівкласична гравітація не оперує гравітонами.
І останнє: геометризація гравітації працює тільки доти, доки діє так званий слабкий принцип еквівалентності: гравітація впливає на всі об'єкти однаково, тому геометричне перетворення в прискорювану систему відліку може локально усунути гравітацію.
Тобто кабіна ліфта, що вільно падає, у гравітаційному полі й та сама кабіна, що ширяє в глибокому космосі, здаються однаковими для тих, хто перебуває всередині, якщо в них немає зовнішнього орієнтира.
Тому деякі фізики шукають альтернативну теорію гравітації, де порушується слабкий принцип еквівалентності.
Тож, найімовірніше, Ейнштейн і Фейнман мають рацію одночасно.
