Після того як 1915 року Альберт Ейнштейн презентував загальну теорію відносності, вона витримала практично всі експериментальні випробування.
ЗТВ змінила наше розуміння гравітації. Раніше вважалося, що ми маємо справу із силою тяжіння між масивними об'єктами. Однак виявилося, що гравітація - це наслідок того, як викривляється простір і час за присутності маси та енергії.
Теорія досягла приголомшливих успіхів - від підтвердження того, що світло вигинається під гравітаційним впливом Сонця до спостережень 2019 року, коли вчені зафіксували силует чорної діри. Тому може здатися дивним той факт, що ЗТВ все ще перебуває на стадії розробки.
Незважаючи на рівняння, введені Ейнштейном, а вони стосуються кривизни, спричиненої масивними об'єктами, теорія не пропонує простого або стандартного способу визначення маси об'єкта.
Кутовий момент - міра обертального руху об'єкта в просторі-часі - є ще більш складно дефініційованим поняттям.
Деякі труднощі пов'язані з петлею зворотного зв'язку, яка вбудована в ЗТВ. Згідно з теорією, матерія та енергія викривляють просторово-часовий континуум, але така кривизна сама по собі перетворюється на джерело енергії, яка може спричинити додаткове викривлення, - явище, яке іноді називають "гравітацією гравітації".
І немає жодного способу відокремити притаманну об'єкту масу від додаткової енергії, що виникає нелінійним ефектом. Ба більше, неможливо визначити імпульс або кутовий момент, попередньо не операціоналізуючи поняття "маса".
Ейнштейн усвідомлював труднощі, пов'язані з кількісним визначенням маси, але так і не зміг повністю сформулювати, чим вона є і як її можна виміряти.
Тільки наприкінці 1950-х - на початку 1960-х років було запропоновано сувору дефініцію. Фізики Річард Арновітт, Стенлі Дезер і Чарльз Міснер визначили масу ізольованого об'єкта, наприклад, чорної діри, як масу нескінченно великої відстані, де простір-час - це "плоска" реальність, а гравітаційний вплив об'єкта наближається до нуля.
Хоча цей спосіб обчислення маси виявився корисним, він не дозволяє вийти на кількісні визначення в межах кінцевої області.
Припустимо, фізики вивчають дві чорні діри, які перебувають у процесі злиття, і хочуть визначити масу кожного окремого чорного тіла, але не всієї системи в цілому. Маса, укладена всередині області і виміряна по її поверхні, де гравітація і викривлення простору-часу гранично сильні, називається "квазілокальною масою".
У 2008 році математики Му-Тао Ванг з Колумбійського університету і Шінг-Тунг Яу, нині професор Університету Цинхуа, Китай, запропонували визначення квазілокальної маси, яке виявилося особливо плідним.
У 2015 році фізики визначили квазілокальний кутовий момент. А навесні цього року вони опублікували дослідження, в якому кутовий момент визначається як "супертрансляційно інваріантний", тобто не залежний від того, де перебуває спостерігач або яку систему координат він обирає. Таке визначення дає змогу вимірювати пульсації в просторі-часі, створювані обертовим об'єктом, а також обчислювати точну кількість кутового моменту, що забирається від об'єкта гравітаційними хвилями.
"Чудовий результат, - каже Лідія Бієрі, математик і експерт із загальної теорії відносності, Мічиганський університет, - і кульмінація складних математичних досліджень, які проводилися протягом кількох років".
Дійсно, на розробку цих аспектів загальної теорії відносності пішли не просто роки, а багато десятиліть.
Визначення квазілокальної маси
У 1960-х роках Стівен Гокінг вигадав визначення квазілокальної маси, яке, завдяки своїй простоті, досі є найкращим. Прагнучи обчислити масу, укладену в горизонті подій чорної діри, він припустив, що її можна обчислити за ступенем вигину світлових променів, що входять і виходять, які перебувають під дією матерії та енергії, що містяться у сфері.
Хоча "масу Гокінга" легко обчислити, це визначення працює тільки у сферично симетричному просторі-часі (оскільки в реальному світі немає нічого ідеально круглого) або у "статичному" (і доволі нудному) просторі-часі, де нічого не змінюється в часі.
Пошуки більш універсального визначення тривали. У своїй лекції 1979 року (Прінстонський університет) британський фізик Роджер Пенроуз назвав задачу визначення квазілокальної маси - "коли не потрібно йти "до нескінченності", щоб поняття було осмислено визначено" - невирішеною проблемою загальної теорії відносності. Визначення квазілокального кутового моменту посіло друге місце в списку Пенроуза.
Раніше того ж року Яу і професор Стенфордського університету Річард Шоен довели основну умову створення квазілокальних визначень. Вони показали, що маса ізольованої фізичної системи, виміряна з нескінченно великої відстані, ніколи не може бути негативною.
Теорема Шен-Яу про "позитивну масу" стала першим важливим кроком у визначенні квазілокальної маси та інших фізичних величин, оскільки простір-час і все, що в ньому знаходиться, буде нестабільним, якщо його енергія не має межі.
У 1989 році австралійський математик Роберт Бартнік запропонував нове визначення квазілокальної маси, яке спиралося на теорему Шен-Яу. Ідея Бартника полягала в тому, що необхідно взяти ділянку кінцевого розміру, оточену поверхнею, а потім, покриваючи її множинними шарами поверхонь дедалі більшої площі, розширити кінцеву ділянку до нескінченного розміру, - і таким чином обчислити її масу.
Але подібна область може бути розширена різними способами, точно так само, як площу поверхні повітряної кулі можна рівномірно роздути або розтягнути в протилежних напрямках, кожен з яких дає відмінну масу.
Найменше значення маси, за словами Бартника, і є квазілокальною масою.
"Цей аргумент був би неможливий до появи теореми позитивної маси, - пояснює Ванг, - тому що в іншому разі маса могла б піти в негативну нескінченність", а мінімальну масу ніколи не могли б встановити.
Маса Бартника була важливою концепцією в математиці, каже математик Лан-Хсуан Хуан з Університету Коннектикуту, але її головний недолік - практичний: знайти мінімум надзвичайно складно.
Фізики Девід Браун і Джеймс Йорк у 1990-х роках запропонували зовсім іншу стратегію. Вони обернули фізичну систему в двовимірну поверхню, а потім спробували визначити масу всередині цієї поверхні на основі її кривизни. Однак одна з проблем методу Брауна-Йорка полягає в тому, що він може дати невірну відповідь в абсолютно плоскому просторі-часі: квазілокальна маса позитивна навіть тоді, коли "має бути" нульовою.
Проте, цей підхід було використано в роботі Ванга і Яу 2008 року. Ґрунтуючись на концепції Брауна і Йорка, а також на дослідженнях, які Яу проводив разом із математиком із Колумбії Мелісою Лю, Ванг і Яу знайшли спосіб обійти проблему позитивної маси в абсолютно плоскому просторі.
Вони виміряли кривизну поверхні у двох різних умовах: у "природному" просторі-часі, що представляє наш Всесвіт (де кривизна доволі складна), і в "еталонному" просторі Мінковського, що є ідеально плоским, оскільки позбавлений матерії.
Будь-яка відмінність у кривизні між цими двома параметрами, за їхнім припущенням, має бути зумовлена масою, що міститься в межах поверхні - іншими словами, квазілокальною масою.
Остання дефініція задовольняє "всім вимогам, необхідним для правильного визначення квазілокальної маси", пишуть вони у своїй статті.
Проте їхній підхід страждає однією особливістю, яка обмежує його застосування: "незважаючи на те, що наше визначення дуже точне, - каже Ванг, - воно вимагає розв'язання кількох дуже складних нелінійних рівнянь. Цей підхід гарний у теорії, але часто виснажливий на практиці".
Кутовий момент
У 2015 році Ванг і Яу спільно з По-Нін Ченом з Каліфорнійського університету поставили собі за мету визначити квазілокальний кутовий момент.
У класичній механіці кутовий момент об'єкта, що рухається по колу, визначається як маса об'єкта, помножена на його швидкість і радіус кола. Це корисна величина для вимірювання, оскільки проходить між об'єктами, але ніколи не створюється і не зникає.
Фізики можуть відстежувати, як кутовий момент обмінюється між об'єктами і навколишнім середовищем, щоб отримати уявлення про динаміку системи.
Щоб визначити квазілокальний кутовий момент, укладений у поверхні, Вангу, Яу і Чену знадобилися дві речі: визначення квазілокальної маси, яке в них було, а також детальне знання того, як обертання працює в просторі-часі.
Спочатку вони помістили свою поверхню в найпростіше можливе середовище - простір-час Мінковського, обраний тому, що він безпомилково плоский і має властивість обертальної симетрії, де кожен напрямок виглядає однаково.
Обертальна симетрія дала змогу визначити квазілокальний кутовий момент як незалежний від місцезнаходження початку координат, що використовується для вимірювання швидкостей і відстаней (початок координат - це точка перетину осей x, y, z і t).
Далі вони встановили відповідність один-до-одного між точками на поверхні в просторі-часі Мінковського і точками на тій самій поверхні у вихідному просторі-часі, тим самим забезпечивши координатну незалежність і в останньому випадку.
Після чого тріо об'єднало зусилля з Е-Каї Вангом з Національного університету Ченг Кунг для розв'язання проблеми, яка залишалася невирішеною близько 60 років: як охарактеризувати кутовий момент, який забирають гравітаційні хвилі, наприклад, ті, що випромінюють дві чорні діри, закручені в спіраль?
Їхнє визначення квазілокального кутового моменту не підходить для обраної задачі, оскільки вимірювання мають проводитися далеко від виру, а не в безпосередній близькості від місця злиття чорних дір.
Відповідна точка огляду називається "нульовою нескінченністю", - поняття, придумане Пенроузом, - і яке стосується кінцевого пункту призначення вихідного випромінювання, як гравітаційного, так і електромагнітного.
Як це часто буває в загальній теорії відносності, виникає нове ускладнення: кутовий момент, який переносять гравітаційні хвилі, навіть якщо його виміряно на нульовій нескінченності, може здаватися таким, що змінюється залежно від вибору початку й орієнтації системи координат спостерігача.
Складність виникає через "ефект пам'яті гравітаційних хвиль" - той факт, що коли гравітаційні хвилі проходять через простір-час, вони залишають постійний відбиток. Хвилі розширюють простір-час в одному напрямку і стискають його в ортогональному напрямку (саме цей сигнал виявляють гравітаційно-хвильові обсерваторії, як-от LIGO і Virgo), але простір-час ніколи не повертається точно у вихідний стан.
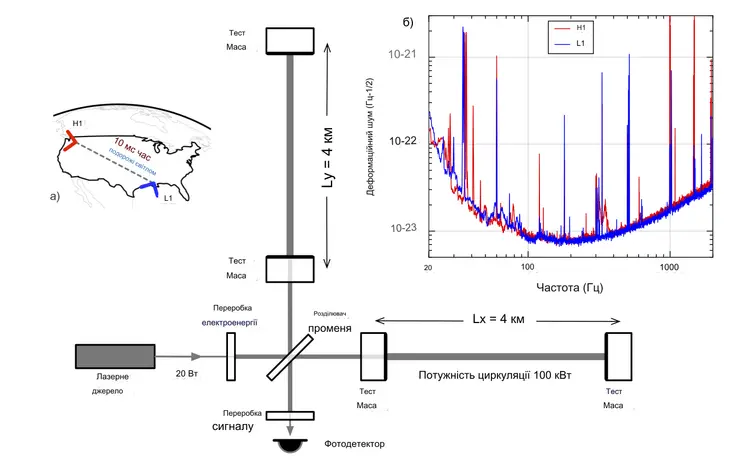
"Гравітаційні хвилі, що проходять, змінюють відстань між об'єктами, - пояснює Еанна Фланаган, релятивіст із Корнельського університету. - Хвилі також можуть трохи перемістити спостерігачів... але вони не знатимуть, що їх перемістили".
Це означає, що навіть якщо різні спостерігачі спочатку згодні з місцезнаходженням початку їхньої системи координат, вони не погодяться з тим, як гравітаційні хвилі перемістять усе навколо.
Зі свого боку, така невизначеність призводить до неоднозначності, "суперпереміщень", у відповідних оцінках кутового моменту.
Інший спосіб зрозуміти суперпереміщення полягає в тому, що хоча ні маса об'єкта, ні його швидкість не спотворені гравітаційною хвилею, яка проходить повз, радіус обертального руху однаково буде спотворений.
Залежно від орієнтації радіуса щодо своєї системи координат, він може здаватися розтягнутим гравітаційним випромінюванням або стисненим, що означає різні можливі визначення кутового моменту.
Збережені фізичні величини не повинні змінюватися або здаватися такими залежно від вибору позначення. Саме цю ситуацію сподівалися виправити Чен, Ванг і Яу. Починаючи з визначення квазілокального кутового моменту, даного 2015 року, вони обчислили кутовий момент, що міститься в області кінцевого радіуса. Потім взяли межу цієї величини при збільшенні радіусу до нескінченності, що перетворило координатно-незалежне квазілокальне визначення на супертрансляційно інваріантну величину на нульовій нескінченності.
За допомогою цього першого в історії супертрансляційно-інваріантного визначення кутового моменту, опублікованого в березні в журналі Advances in Theoretical and Mathematical Physics, можна в принципі визначити кутовий момент, який виноситься гравітаційними хвилями, випущеними під час зіткнення чорних дір.
"Це чудова стаття і чудовий результат, - упевнений Маркус Хурі, математик з Університету Стоні Брук, Нью-Йорк, - але питання в тому, наскільки він корисний".
Він пояснив, що нове визначення абстрактне і важко обчислюване, "а фізикам, взагалі кажучи, не подобаються речі, які важко обчислювати".
Неминуча властивість кутового моменту
Складність обчислень, однак, є майже неминучою особливістю загальної теорії відносності. Зазвичай навіть важко розв'язати нелінійні рівняння, які Ейнштейн сформулював у 1915 році, за винятком симетричних ситуацій.
Замість цього дослідники покладаються на суперкомп'ютери для отримання наближених рішень. Вони роблять проблему розв'язуваною, розбиваючи простір-час на дрібні сітки й оцінюючи кривизну кожної сітки окремо і в окремі моменти часу. Наближені рішення стають дедалі кращими в міру додавання нових сіток - подібно до додавання нових пікселів у телевізорі високої чіткості.
Ці наближення дають змогу дослідникам розрахувати маси і кутові моменти чорних дір або нейтронних зірок, що зливаються. Розрахунки проводяться на основі сигналів гравітаційних хвиль, виявлених обсерваторіями LIGO і Virgo.
За словами Віджая Варми, фізика з Інституту гравітаційної фізики Макса Планка, сучасні спостереження гравітаційних хвиль недостатньо точні, щоб тонкі відмінності, спричинені суперпереміщеннями, були помітні.
"Але коли точність наших спостережень підвищиться в 10 разів, ці міркування стануть більш важливими", - вважає Варма. Він зазначив, що поліпшення такого порядку можуть бути реалізовані вже у 2030-х роках.
Фланаган дотримується іншої точки зору, стверджуючи, що суперпереміщення - це "не проблема, яку потрібно розв'язувати", а радше неминуча властивість кутового моменту в загальній теорії відносності, з якою нам доведеться жити.
Фізик Роберт Волд, фахівець із загальної теорії відносності з Чиказького університету, певною мірою поділяє точку зору Фланагана, кажучи, що супертрансляції - це радше "незручність", ніж реальна проблема.
Проте, він уважно вивчив статтю Чена, Ванга і Яу і дійшов висновку, що доказ добре тримається.
"Воно справді вирішує неоднозначність суперпереміщення", - пояснює Волд, додавши: "У загальній теорії відносності, коли у вас є всі ці альтернативні визначення на вибір", приємно мати "унікальний вибір", який можна вибрати".
Яу, який працює над визначенням цих величин із 1970-х років, дотримується довгострокової перспективи.
"Може пройти багато часу, перш ніж ідеї з математики проникнуть у фізику".
Він зазначив, що навіть якщо нове визначення кутового моменту поки що залишиться невикористаним, вчені з LIGO і Virgo "завжди обчислюють щось приблизно". Але в кінцевому рахунку, добре знати, що це за річ, яку ви намагаєтеся наблизити".
