Знак равенства является основой математики. Кажется, что это совершенно фундаментальное и неоспоримое утверждение. Как и тождественность равенства и математического взгляда на окружающий мир.
Але вже кристалізується ціла спільнота математиків, яка розглядає знак рівності як первісну помилку "точних наук". На їхню думку, саме "=" апріорі задає непереборні складнощі в тому, як співвідносяться величини: на малому, "повсякденному" рівні "рівність" ще працює, а ось коли задаються складні множини або величини, тоді виникають проблеми.
Тому "відступники" хочуть переформулювати математику більш вільною мовою еквівалентності. "Ми вигадали це поняття рівності", - переконаний Джонатан Кемпбелл з Університету Дьюка, - Насправді ми маємо оперувати поняттям "еквівалентність".
Найвидатніша постать у цій спільноті - Джейкоб Лур'є. У липні цього року 41-річний математик змінив свою штатну посаду в Гарвардському університеті на посаду викладача в Інституті перспективних досліджень у Прінстоні, штат Нью-Джерсі, де мешкає багато хто з найбільш шанованих математиків у світі.
Ідеї Лур'є поширюються в масштабі, що рідко трапляється в будь-якій галузі. За допомогою своїх книг, які являють собою тисячі щільних технічних сторінок, він розробив зовсім інший спосіб інтерпретації базових понять у математиці, відмовляючись від знака рівності.
Лур'є опублікував свою першу книгу "Теорія вищих топосів" у 2009 році. Том із 944 сторінок слугує керівництвом для понятійного транзиту усталених галузей математики на нову мову "нескінченних категорій".
Відтоді ідеї Лур'є знайшли широкий відгук серед учених, пов'язаних із математичними дисциплінами. Багато математиків вважають їх незамінними для формування майбутнього поля практичних досліджень. Проте поширення категорій нескінченності також виявило зростаючі болі, яких зазнає така математика щоразу, коли вона намагається поглинути велику нову ідею, що кидає виклик сенсу її попереднього існування.
"У математичному співтоваристві домінує відповідний рівень консервативності", - каже Кларк Барвік з Единбурзького університету. - Я просто не думаю, що ви можете очікувати, що якась група математиків прийме новий інструмент, не отримавши переконливих причин для цього".

Хоча багато математиків прийняли категорії нескінченності, відносно мало хто повністю прочитав довгі, дуже абстрактні тексти Лур'є. У результаті деякі роботи, засновані на його ідеях, менш суворі, ніж зазвичай прийнято в математиці. Математики, як і раніше, стикаються як з неймовірними масштабами ідей Лур'є, так і з тим унікальним способом, у який вони були представлені.
Перепакування в більш тривіальні форми, щоб зробити їх доступними для більшої кількості математиків, також негативно позначається на розумінні вихідних точок пропонованої парадигми. Яскрава математична революція перетворюється на буденний закон. Проте вони будують майбутнє математики, засноване не на рівності, а на еквівалентності.
Вежі еквівалентності
Математична рівність, можливо, може здатися найменш спірною із запропонованих ідей. Дві намистинки плюс одна намистина дорівнює трьом. Що ще можна сказати з цього приводу? Але найпростіші ідеї можуть бути найпідступнішими. З кінця 19-го століття математика будувалася на ідеї множин. Теорія множин задає правила або аксіоми для побудови і маніпулювання цими множинами.
Сучасні підходи, як квантова геометрія, вимагають перегляду цих аксіом, наближаючись до ідей Лур'є про еквівалентність у просторі квантових станів.
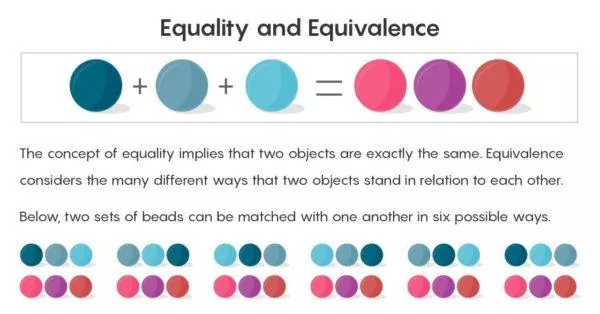
Наприклад, одна з цих аксіом говорить, що ви можете додати до набору з двома елементами ще набір з одним елементом, щоб створити нову множину з трьома елементами: 2 + 1 = 3. На формальному рівні спосіб показати, що дві величини рівні, полягає в їхньому сполученні: зіставте одну кульку з правого боку знака рівності з аналогічною кулькою з лівого боку. Зверніть увагу, що після того, як додавання здійснено, намистин більше не залишилося.
Теорія множин визнає, що два набори з трьома об'єктами в кожній парі точні, але вона не легко сприймає різні способи створення пар. Ви можете з'єднати першу кульку праворуч із першою ліворуч або першу праворуч із другою ліворуч і т. д. (загалом існує шість можливих поєднань). Сказати, що два плюс один дорівнює трьом, і залишити все як є, значить випустити з уваги всі різні способи, якими вони тотожні.
"Проблема в тому, що є багато способів з'єднатися, - пояснює Кемпбелл. - Ми забули про них, коли говоримо "дорівнює".
Ось тут-то і закрадається еквівалентність. Хоча рівність - це суворі відносини - або дві речі рівні, або ні - еквівалентність імовірнісна в різних формах. Коли ви можете точно зіставити кожен елемент одного набору з елементом іншого, тоді ми говоримо про сильну форму еквівалентності.
Але в галузі математики, яка називається теорією гомотопій, наприклад, дві форми (або геометричні простори) еквівалентні, якщо одна з них розтягується або стискається в іншу, не розрізаючи і не розриваючи її. З точки зору теорії гомотопій, плоский диск і одна точка в просторі еквівалентні - ви можете стиснути диск до точки. Однак неможливо з'єднати точки на диску з точками в точці.
Зрештою, на диску нескінченна кількість точок, а точка - лише одна. Із середини 20-го століття математики намагалися розробити альтернативу теорії множин, за допомогою якої можна проводити розрахунки на основі принципу еквівалентності. У 1945 році математики Семюель Ейленберг і Сондерс Мак Лейн представили новий фундаментальний об'єкт, у якому здійснювалася еквівалентність. Вони назвали цей об'єкт "категорією". Категорії можуть бути заповнені чим завгодно. У вас може бути категорія ссавців, яка вбирає в себе всіх істот у світі, які мають шерсть, теплокровних, які годують молоком.
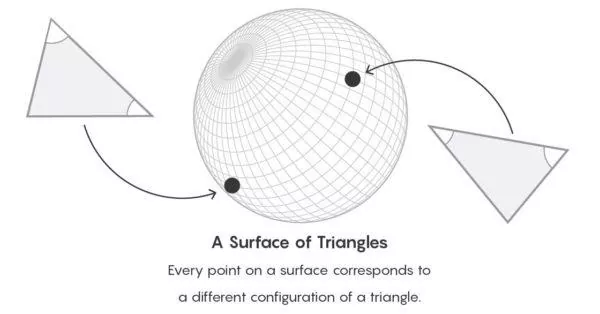
Або ви можете створювати категорії математичних об'єктів: множини, геометричні простори або системи числення. Категорія - це набір із додатковими метаданими: опис усіх способів, якими два об'єкти взаємопов'язані, і включає опис усіх способів отримання еквівалентності. Геометричні категорії спрощуються до ймовірного комбінування точок. Уявіть собі, наприклад, поверхню земної кулі. Тут кожна точка являє собою трикутник іншого типу. Шляхи між цими точками виражають відносини еквівалентності між об'єктами. З погляду теорії категорій, ви забуваєте про явний спосіб опису будь-якого одного об'єкта і замість цього зосереджуєтеся на топології окремого класу об'єктів.
"Є багато речей, про які ми думаємо як про речі, коли вони насправді є відносинами між речами", - стверджує математик Ірина Захаревич. - Фразу "мій чоловік" ми розглядаємо як об'єкт, але це і відношення до мене". Версія категорій Ейленберга і Мак Лейна добре підходила для відстеження сильних форм еквівалентності. Але в другій половині 20-го століття математики частіше концентрувалися на описі слабких еквівалентностей, таких, як гомотопії. "У міру того, як математика стає дедалі тоншою, неминуче відбувається прогрес у вивченні тонших понять тотожності", - каже Емілі Ріл, математик з Університету Джона Гопкінса.
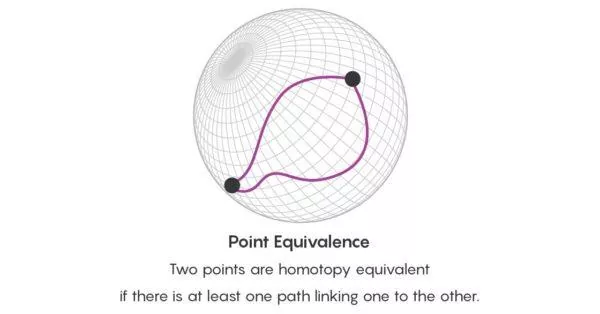
У цих більш тонких поняттях еквівалентності кількість інформації про те, як пов'язані між собою два різні об'єкти, різко зростає. Елементарні категорії Ейленберга і Мак Лейна не були призначені для такого роду операцій. Щоб побачити, як збільшується обсяг інформації, спочатку згадайте нашу сферу, яка являє собою безліч трикутників. Два трикутники гомотопічно еквівалентні, якщо вони взаємодеформовані. Дві точки на поверхні гомотопічно еквівалентні, якщо є шлях, що зв'язує одну з іншою. Вивчаючи гомотопічні шляхи між точками на поверхні, отримуємо різні способи взаємозв'язку трикутників, представлених цими точками.
Але недостатньо сказати, що дві точки взаємопов'язані безліччю рівних шляхів. Потрібно ще вирішити питання про еквівалентність між усіма цими шляхами. Таким чином, на додаток до питання про те, чи еквівалентні дві точки, ви тепер запитуєте, чи еквівалентні два шляхи, що починаються й закінчуються в одній і тій самій парі точок, тобто чи існує домінуючий шлях між цими шляхами. Цей шлях між шляхами набуває форми диска, межа якого і визначається двома шляхами. Також пропонується інший сценарій.
Два диски еквівалентні, якщо між ними є шлях, і цей шлях набуде форми тривимірного об'єкта. Ці тривимірні об'єкти самі можуть бути пов'язані чотиривимірними шляхами (шлях між двома об'єктами завжди має на один вимір більше, ніж самі об'єкти). Уточнимо, що пропонована модель не враховує фактора часу, що докорінно спрощує завдання.
Зрештою, ви побудуєте нескінченну вежу еквівалентностей між еквівалентностями. Тільки в такому разі зведена будівля створює повне уявлення про будь-які об'єкти, обрані для представлення як точки на цій сфері. "Це просто сфера, але, виявляється, щоб зрозуміти форму сфери, потрібно в деякому сенсі вийти на нескінченність", - пояснює Девід Бен-Цві з Техаського університету в Остіні.
Переписування математики
Перша робота Джейкоба Лур'є з теорії категорій нескінченності виявилася провальною. 5 червня 2003 року 25-річний хлопець розмістив 60-сторінковий документ "Про нескінченність топосів" на arXiv.org. Там же він окреслив нові правила, за якими математики можуть працювати з категоріями нескінченності. Ця перша стаття була погано сприйнята. Незабаром після її публікації прочитання Пітер Мей, математик із Чиказького університету, надіслав електронного листа науковому керівнику Лур'є Майклу Хопкінсу, в якому йшлося про те, що хоча у статті молодого науковця були цікаві ідеї, але сама теорія є попередньою та потребує більшої строгості.
Невідомо, чи сприйняв Лур'є лист Мей як виклик, чи самостійно розвивав свої думки. Зрозуміло тільки, що після отримання листа Лур'є випустив кілька книг, які лягли в основу цілого математичного руху. У 2006 році Лур'є опублікував на arXiv.org проєкт з теорії вищих топосів. У цій гігантській роботі він описав модель, необхідну для заміни теорії множин новою математичною основою, заснованою на нескінченних категоріях. Потім у 2011 році Лур'є запропонував іншу роботу, яка заново перезапускає алгебру.
Остання являє собою прекрасний набір формальних правил для маніпулювання рівняннями. Математики постійно використовують ці правила для доведення нових теорем. Але алгебра пропонує числову еквілібристику, обмежену знаком рівності. Якщо видалити схоластику рівності на концепцію еквівалентності, більшість простих математичних операцій ускладниться. Приміром, перші правила алгебри, які діти вчать у школі: сума або добуток трьох або більше чисел не залежить від того, як згруповані числа: 2 × (3 × 4) = ( 2 × 3) × 4.
Доведення того, що асоціативна властивість виконується для будь-якого списку з трьох або більше чисел, легко, коли ви працюєте з рівністю. Але складно, коли оперуєте поняттями еквівалентності. Особливо коли ви переходите до більш тонких понять еквівалентності з їхніми нескінченними вежами шляхів між шляхами, навіть просте правило, таке як асоціативна властивість, перетворюється на непрохідний ліс.
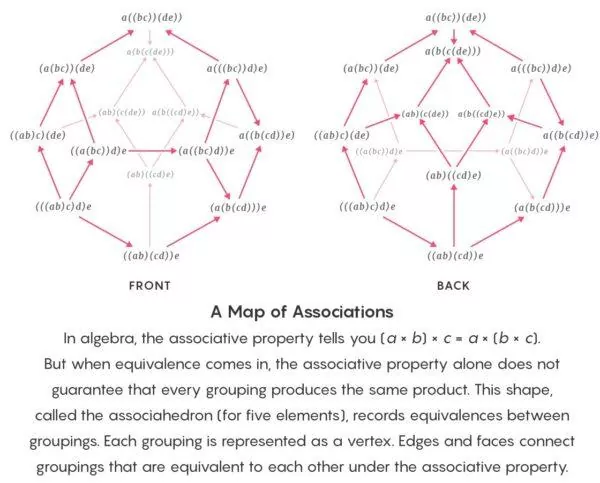
У "Вищій алгебрі", остання версія якої налічує 1553 сторінки, Лур'є розробив версію асоціативної властивості для категорій нескінченності, а також багато інших алгебраїчних теорем, що в сукупності створили основу для математики еквівалентності. Однак революції вимагають часу, а, як показують книги Лур'є, наступні роки можуть бути хаотичними для "звичної" математики.
Перевчитися
Ясне мислення - стійкий атрибут математиків: докази правильні чи ні, ідея працює чи ні. Але професорські та інші посади обіймають люди, і якраз вони реагують на нові ідеї - суб'єктивно, емоційно і зацікавлено. У цьому відношенні робота Лур'є становила велику проблему. У глибині душі виникала підозра про інтелектуальну провокацію. Мовляв, ось він найкращий спосіб зробити математику і математиків. Але теорія поки що розрахована виключно на методологів.
Якщо математична революція відбудеться в найближчому майбутньому, то перебудова всієї конструкції займе дуже тривалий час - від переписування всієї математики до оновлення фізики й астрономії, від школи до академічних методів навчання. Можливо, хотів того Лур'є чи ні, але він запустив каток, здатний розчавити в нуль майже всю історію так званих точних наук. Роботу Лур'є поки що складно засвоїти "в спокійній обстановці". Обсяг матеріалу настільки великий, що математики мають витратити роки на навчання, не кажучи вже про перенавчання.
Непідйомне завдання для вчених середнього рівня і ризиковане для аспірантів, у яких є лише кілька років, щоб отримати результати, які допоможуть їм знайти пристойну роботу. Як і багато нових винаходів, теорія вищих топосів вимагає, щоб математики постійно співвідносили свої висновки з методологією, яка змушує працювати теорію.
Це все одно що змусити кожного 16-річного спочатку навчитися відновлювати двигун, а потім видати права. Тільки от біда - права доведеться також переробляти, вписувати принципово нові дані, про які, своєю чергою, мало що відомо внаслідок граничної абстрактності праць Лур'є. Проте виклик традиційній математиці кинуто. І, схоже, академічна наука прийняла виклик. Хоча в професорських кабінетах не зовсім чітко розуміють, як теорія вищих топосів позначиться на звичній фізиці, хімії, астрономії, геології.
Та й навіщо їм думати? Вони книжок не читають.
P.S.
Насправді Джейсон Лур'є спровокував "гомотопічну революцію", зробивши інструменти та ідеї гомотопічної алгебри доступними для широкої аудиторії.
Наприклад, він створив геометричну мову langlands, яка допомагає звичайним людям формулювати проблемні твердження без зайвих зусиль.
Інший приклад - параметризована теорія гомотопії: на випадок якщо ви бажаєте прикріпити до простору якийсь гаджет у певний зв'язний спосіб.
Разом із тим Лур'є не створює абстрактну магію, яка вирішує всі людські проблеми. Його математичний апарат може допомогти швидше дістатися до суті питань або вирішити технічні проблеми, але, врешті-решт, нам все одно доведеться займатися складною математикою.
Джерело: Quanta Magazine