Квантова критична система - це явище, що виникає, коли квантова система зазнає фазового переходу при нульовій температурі, зумовленого квантовими флуктуаціями.
Подібні системи демонструють універсальні властивості, які не залежать від законів масштабування та конформної симетрії. Такі властивості описуються за допомогою конформної теорії поля (КТП), де квантові поля змінюють “частинки” поблизу критичних точок.
Проблеми з квантовою критичністю виникають при ідентифікації КТП та відповідній їй квантовій системі. Традиційно це робиться за допомогою алгебраїчних методів, які залучають оператори та симетрії КТП.
Однак сучасний математичний апарат не застосовується до наближених КТП, тобто до квантових систем, близьких до критичності, - в першу чергу слабо збурених КТП або ґраткових моделей, які наближаються до КТП в межах континууму.
У нещодавній статті, опублікованій в Physical Review Letters, група дослідників з Каліфорнійського університету в Берклі запропонувала новий метод для опису одновимірних (1D) квантових критичних систем, що використовує ентропію заплутаності та гамільтоніан заплутаності. Метод дозволяє виміряти квантові кореляції між різними частинами системи.
Нагадаємо, ентропія заплутаності - це кількість інформації, яка втрачається при відстеженні частини системи, тоді як гамільтоніан заплутаності - це оператор, здатний генерувати динаміку заплутаності.
Автори показали, що основний стан одномірної унітарної ККС, що зберігає ймовірність квантових станів, задовольняє набір ентропійних умов, які пов'язують ентропію заплутаності та гамільтоніан заплутаності різних інтервалів на системі.
Наявні умови не залежать від ультрафіолетового відсікання. Вон також виконуються для 1D щілинних фаз у фіксованих точках групи перенормування, квантових систем, що не змінюються при перетвореннях.
Автори також припускають, що ентропійні умови достатні та необхідні для опису основних станів 1D RG нерухомих точок з симетрією Лоренца. Остання пов'язує різні інерціальні системи відліку.
Дослідники також вивели кілька наслідків - властивості масштабування глобальних конформних генераторів та алгоритм відновлення локальних гамільтоніанів ККС.
Довідка:
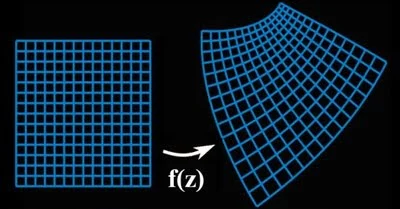
Конформна теорія поля вивчає системи з симетріями відносно перетворень простору-часу, які зберігають кути між кривими лініями, але можуть змінювати їх довжини.
Приклади конформних перетворень - зсуви та спеціальні перетворення Лоренца.
КТП має багато застосувань у різних галузях фізики - статистична механіка, фізика конденсованих середовищ, теорія струн, космологія та гравітація.
Теорія дозволяє розв'язувати деякі складні задачі, які не можуть бути розв'язані звичайними методами пертурбацій. Що пов'язано з вимогами високої ступені симетрії та обмеження кореляційних функцій та операторів.
Крім того, конформна теорія поля має багато елегантних математичних структур, таких як алгебра Вірасоро, алгебра Каца-Муди, модульні форми та грасманіани.
Особливо цікавим вважається окремий випадок двовимірної КТП, де локальні конформні перетворення утворюють нескінченновимірну групу.
Що, своєю чергою, призводить до виникнення нескінченного числа збережених зарядів, які називаються конформними вагами.
Конформні ваги визначають аномальні розмірності операторів; вони відіграють роль мас у двовимірній КТП.
Також конформні ваги визначають спектр станів теорії, який класифікується за допомогою модульної інваріантності - незмінності відносно дискретних перетворень параметрів самої теорії.
