
У минулому столітті квантова теорія поля здавалася наймасштабнішою та найуспішнішою фізичною теорією. Вона нагадувала парасольку, що охоплює більшість теорій поля. Найвідоміший приклад - Стандартна модель, розкручена в науковому співтоваристві в 50-60-х роках минулого століття.
"На фундаментальному рівні вона здатна пояснити буквально кожен експеримент, який ми коли-небудь проводили", - каже Девід Тонг, фізик із Кембриджського університету.
Але квантова теорія поля, безперечно, неповна. Ні фізики, ні математики не знають, що саме робить КТП квантовою теорією поля. У них є проблиски повної картини, але вчені поки що не можуть у них розібратися.
 "Існують різні ознаки того, що таке КТП", - каже Натан Сейберг, фізик з Інституту перспективних досліджень. - Таке відчуття, що це тварина, яку можна доторкнутися з багатьох боків, але ви не побачите її цілком".
"Існують різні ознаки того, що таке КТП", - каже Натан Сейберг, фізик з Інституту перспективних досліджень. - Таке відчуття, що це тварина, яку можна доторкнутися з багатьох боків, але ви не побачите її цілком".
Математика перетворює будь-яку гіпотезу на наукову теорію. Якщо математика навчиться описувати квантову теорію з тією ж суворістю, з якою вона характеризує добре відомі математичні об'єкти, то ми зіштовхнемося з більш повною картиною фізичного світу.
Кожна фізична ідея має своє природне місце в математиці. Це стосується і квантової теорії поля.
Тепер дослідники мають намір математично визначити, взявши ідеї, об'єкти і методи, які фізики розробили для вивчення фундаментальних частинок, і включили їх в основний корпус математики. Це означає створення універсальної математичної моделі, щоб майбутнім математикам не довелося думати про фізичний контекст самої теорії.
Винагорода очікується велика: математика розвивається, коли знаходить нові об'єкти для дослідження та нові структури, що відображають найважливіші відносини між числами, рівняннями та формами.
"Сама фізика, як структура, надзвичайно глибока і часто є найкращим способом думати про математичні речі, які нас уже цікавлять. Це просто найкращий спосіб організувати їх", - каже американський математик Девід Бен-Цві.
Протягом 40 років КТП спокушала нереалізованими ідеями. Останніми роками з'явилася можливість описувати сутності, абстрагуючи їх від світу фізики частинок у самостійні математичні об'єкти.
"Ми нічого не дізнаємося, поки не доберемося до мети, але я очікую, що ми бачимо тільки верхівку айсберга", - каже фізик Грег Мур.
Поля назавжди
Прийнято вважати, що Всесвіт побудовано з фундаментальних частинок: електронів, кварків, фотонів тощо. Але фізики вже давно відійшли від цього уявлення. Замість частинок існують "квантові поля", які сприймаються більш реалістично, ніж "звичайні" частинки.

Ці поля простягаються через увесь простір-час Всесвіту. Вони мають безліч різновидів і коливаються подібно до бурхливого океану. У міру того, як поля пульсують і взаємодіють одне з одним, з них з'являються частинки, а потім знову зникають, як швидкоплинні гребені хвилі.
"Частинки - це не об'єкти, які існують вічно, - каже Тонг. - Це танець полів".
Щоб зрозуміти квантові поля, найпростіше описати класичне поле. Уявіть собі вимірювання температури в кожній точці земної поверхні. Поєднання нескінченно великої кількості точок, у яких можна зробити ці вимірювання, утворює геометричний об'єкт, званий полем, де зібрана вся інформація про температуру.
Поля виникають щоразу, коли є якась величина, яку можна однозначно виміряти з нескінченно малою роздільною здатністю.
"Ви ніби можете ставити незалежні одне від одного запитання в кожній точці простору-часу", - каже Давіде Гайотто, фізик з Інституту теоретичної фізики у Ватерлоо, Канада.
Але квантові поля виникають, коли ведуться спостереження за квантовими явищами, наприклад, за енергією електрона.
У той час як температура в будь-якій точці Землі не залежить від того, вимірюєте ви її чи ні, електрони не розташовуються в конкретному місці до моменту спостереження. Їхнє становище описується тільки імовірнісно, шляхом присвоєння кожній точці квантового поля значень, що відображають довільну ймовірність того, що електрон перебуває саме там, де його "помістили". До спостереження електрони, по суті, ніде не існують - і одночасно перебувають скрізь.
"Більшість речей у фізиці - це не просто об'єкти; це щось, що живе в кожній точці простору і часу", - каже директор Інституту перспективних досліджень Робберт Дейкграаф.
Квантова теорія поля передбачає набір певних правил, кореляційних функцій, які пояснюють, як вимірювання в одній точці поля співвідносяться з вимірюваннями, зробленими в іншій точці.
Кожна КТП описує фізику точної кількості вимірювань:
- двовимірні КТП часто корисні для опису поведінки матеріалів, наприклад, ізоляторів;
- шестивимірні квантові теорії особливо важливі для теорії струн;
- чотиривимірні описують фізику в спостережуваному всесвіті.
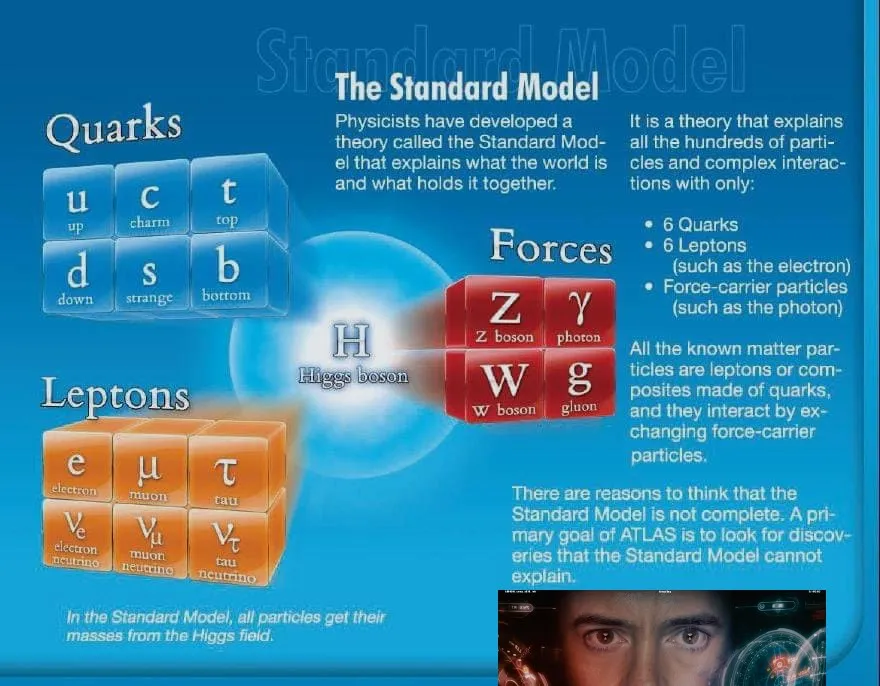
- Стандартна модель - одна з них; це найважливіша квантова теорія поля, тому що саме вона найкраще описує Всесвіт.
Відомі 12 фундаментальних частинок, з яких складається Всесвіт. Кожна з них має своє унікальне квантове поле. До цих 12 полів частинок Стандартна модель додає чотири силові поля, що представляють чотири фундаментальні сили: гравітацію, електромагнетизм, сильні ядерні сили та слабкі ядерні сили. Вона об'єднує ці 16 полів в одне рівняння, яке описує, як вони взаємодіють одне з одним. Завдяки цим взаємодіям фундаментальні частинки розуміються як флуктуації відповідних квантових полів, і перед нашими очима виникає фізичний світ.
Може здатися дивним, але в 1930-х роках вчені дійшли згоди, що фізика, заснована на полях, а не на частинках, розв'язує найгостріші протиріччя, починаючи з питань про причинність і закінчуючи припущенням, що частинки не живуть вічно. Інакше неймовірна сталість у фізичному світі.
"Усі частинки одного типу у Всесвіті однакові, - каже Тонг. - Якщо ми вирушимо на Великий адронний колайдер і створимо щойно викарбуваний протон, він буде точно таким самим, як і той, що мандрував протягом 10 мільярдів років. Це заслуговує на якесь пояснення".
КТП пояснює, що всі протони - це просто флуктуації одного й того ж поля протонів (або, якщо подивитися пильніше, основних полів кварків).
Але пояснювальна сила КТП обходиться у високу математичну ціну.
"Квантові теорії поля - це, безумовно, найскладніші об'єкти в математиці, настільки складні, що математики не мають ані найменшого уявлення про те, як у них розібратися, - пояснює Тонг. - Квантова теорія поля - це математика, яку ще не винайшли математики".
Занадто багато нескінченності
Що ж робить її такою складною для математиків? Одним словом, нескінченність.

Коли ви вимірюєте квантове поле в точці, результат - це не кілька чисел, таких, як координати і температура. Однак загалом виходить матриця, тобто масив чисел. І не просто матриця, а велика матриця, звана оператором, з нескінченно великою кількістю стовпців і рядків. Це відображає те, як квантове поле охоплює всі можливості частинки, що виходять із поля.
"Існує нескінченно багато положень, які може мати частинка, і це призводить до того, що матриця, яка описує вимір положення, імпульсу, також повинна бути нескінченно розмірною", - пояснює Кася Рейзнер з Університету Йорка.
А коли теорії продукують нескінченності, це ставить під сумнів їхню фізичну релевантність, бо нескінченність існує як концепція, а не вимірювання та експеримент. Ця обставина блокує математичну роботу з теоріями.
"Нам не подобається мати рамки, в яких прописана нескінченність. Саме тому ви починаєте розуміти, що необхідне математичне розуміння того, що відбувається", - каже Алехандра Кастро, фізик з Амстердамського університету.
Проблеми з нескінченністю посилюються, коли фізики починають думати про взаємодію двох квантових полів, як, наприклад, під час моделювання зіткнень частинок на Великому адронному колайдері. У класичній механіці такий тип розрахунків простий: щоб змоделювати, що відбувається під час зіткнення двох більярдних куль, досить використовувати числа, що визначають імпульс кожної кулі в точці зіткнення.
Коли два квантові поля взаємодіють, аналогія не спрацьовує: помножити нескінченно розмірний оператор для одного поля на нескінченно розмірний оператор для іншого поля саме в тій точці простору-часу, де вони зустрічаються, погодьтеся, вельми складно. І не факт, що вони зустрічаються в одній точці, - тут виникає додатковий, третій оператор. Такий розрахунок - множення двох-трьох нескінченно-вимірних об'єктів, які розташовані нескінченно близько один до одного - фантастичний.
Приголомшливий успіх
Фізики і математики не можуть обчислювати, використовуючи нескінченності, але вони розробили обхідні шляхи - способи апроксимації величин, які дозволяють обійти цю проблему. Обхідні шляхи дають приблизні передбачення, що досить добре, тому що експерименти теж не нескінченно точні.
"Ми можемо проводити експерименти і вимірювати речі з точністю до 13 знаків після коми, і вони узгоджуються з усіма 13 знаками після коми. Це найдивовижніша річ у всій науці", - каже Тонг.
Один із варіантів вирішення проблеми полягає в тому, щоб уявити квантове поле, де нічого не відбувається. Таку ситуацію описує так звана "вільна" теорія, оскільки вона вільна від взаємодій, а тому не потрібно турбуватися про множення матриць нескінченної розмірності, тому що ніщо не перебуває в русі і ніщо ніколи не стикається. Таку ситуацію легко описати в усіх математичних подробицях, хоча сам опис не становить наукової цінності.
"Це абсолютно нудно, тому що ви описуєте одиничне поле, якому нема з чим взаємодіяти, тож це трошки академічна вправа", - пояснює Рейзнер. Але її можна зробити цікавішою. Фізики посилюють взаємодію, намагаючись зберегти математичний контроль над картиною в міру посилення взаємодії.
Такий підхід називається пертурбативною КТП, у тому сенсі, що допускаються невеликі зміни, або збурення, у вільному полі. Пертурбативну перспективу можна застосовувати до квантових теорій поля, які схожі на вільну теорію. Це також надзвичайно корисно для перевірки експериментів.
"Ви отримуєте дивовижну точність, дивовижну експериментальну узгодженість", - каже Рейзнер.
Але якщо продовжувати посилювати взаємодії, то пертурбативний підхід врешті-решт перегрівається. Замість того, щоб робити все більш точні розрахунки, наближені до реального фізичного всесвіту, він стає все менш точним. Це свідчить про те, що хоча метод збурень є корисним посібником для експериментів, зрештою, це не той спосіб, за допомогою якого описується Всесвіт: він практично корисний, але теоретично хиткий.
"Ми не знаємо, як усе скласти й отримати щось розумне", - підкреслює Гайотто.Інша схема апроксимації намагається підкрастися до повноцінної квантової теорії поля в інший спосіб. У теорії квантове поле містить нескінченно тонку інформацію. Щоб створити такі поля, фізики починають із решітки, або сітки, і обмежують вимірювання місцями, де лінії решітки перетинаються одна з одною. Таким чином, замість того, щоб вимірювати квантове поле скрізь, спочатку його "оцінюють" в окремих точках на фіксованій відстані одна від одної.
Потім учені підвищують роздільну здатність решітки, зближуючи нитки, щоб створити дедалі тонше плетіння. У міру того, як воно ущільнюється, кількість точок, у яких проводять вимірювання, збільшується, наближаючись до ідеалізованого уявлення про поле, у якому проводять вимірювання.
"Відстань між точками стає дуже маленькою, і таким чином виникає безперервне поле", - каже Зайберг. У математичному значенні - межа решітки, що стягується.
Математики звикли працювати з межами і знають, як встановити, що деякі з них дійсно існують. Наприклад, вони довели, що межа нескінченної послідовності 12 + 14 +18 +116 ... дорівнює 1. Фізики хотіли б довести, що квантові поля є межею цієї ґратчастої структури. Але вони не знають, як це зробити.
"Не зовсім зрозуміло, як визначити межу і що вона означає математично", - каже Мур.
 Фізики не сумніваються, що решітка, яка стягується, рухається до ідеалізованого поняття квантового поля. Тісна відповідність між передбаченнями КТП і експериментальними результатами переконливо свідчить про те, що це так.
Фізики не сумніваються, що решітка, яка стягується, рухається до ідеалізованого поняття квантового поля. Тісна відповідність між передбаченнями КТП і експериментальними результатами переконливо свідчить про те, що це так.
"Немає жодних сумнівів у тому, що всі ці межі справді існують, тому що успіх квантової теорії поля був справді приголомшливим, - підкреслює Сейберг. - Але мати переконливі докази того, що щось вірно, і остаточно довести, що це так, - дві різні речі".
Йдеться про ступінь неточності, яка не відповідає іншим великим фізичним теоріям, які КТП прагне перевершити. Закони руху Ісаака Ньютона, квантова механіка, теорії спеціальної та загальної відносності Альберта Ейнштейна - усі вони лише частини великої історії, яку хоче розповісти КТП, але вона поки що не може бути записана в точних математичних термінах.
"Квантова теорія поля виникла як універсальна мова фізичних явищ, хоча й перебуває в поганій математичній формі", - каже Дейкграаф. І для деяких фізиків це привід поставити паузу у своїх теоретичних дослідженнях.
"Якщо весь будинок тримається на основній концепції, яка сама по собі не зрозуміла математично, чому ви так впевнені, що вона описує світ? Це питання", - міркує Дійкграаф.
Геометрія частинки
Навіть у незавершеному стані КТП спровокувала низку важливих математичних відкриттів. Загальна схема взаємодії така: фізики, які використовують КТП, стикаються з дивовижними обчисленнями, які потім намагаються пояснити математики.
"Це машина, що генерує ідеї", - упевнений Тонг.
На базовому рівні фізичні явища тісно пов'язані з геометрією. Можна навести приклад: якщо привести в рух кулю на гладкій поверхні, то її траєкторія покаже найкоротший шлях між будь-якими двома точками - ця властивість відома як геодезія. Таким чином, фізичні явища можуть визначати геометричні особливості форми.
Тепер замінимо більярдну кулю електроном. Електрон існує ймовірно скрізь на довільній поверхні. Вивчаючи квантове поле, яке фіксує ці ймовірності, можна обстежити саму поверхню, наприклад, з'ясувати, скільки в ній отворів. Це фундаментальне питання, на яке хочуть відповісти математики, що працюють у геометрії та суміжній галузі - топології.
Наприкінці 1970-х років фізики і математики почали застосовувати цю перспективу для вирішення основних питань геометрії. До початку 1990-х років Зайберг і його співробітник Едвард Віттен зрозуміли, як її використати для створення нового математичного інструменту - тепер його називають інваріантами Зайберга-Віттена, - який перетворює квантові явища на індекс математичних характеристик форми: підрахуйте, скільки разів квантові частинки поводяться певним чином, і ви ефективно підрахуєте кількість дірок у формі.
"Віттен показав, що квантова теорія поля дає абсолютно несподіване, але абсолютно точне розуміння геометричних питань, роблячи нерозв'язні проблеми розв'язними", - пояснює Грем Сігал, математик з Оксфордського університету.
Інший приклад такого обміну стався на початку 1990-х років, коли фізики проводили розрахунки, пов'язані з теорією струн. "Вимірювання" проводилися у двох різних геометричних просторах, заснованих на принципово різних математичних правилах, але в результаті були отримані довгі набори чисел, які точно відповідали один одному. Так з'явилася абсолютно нова галузь досліджень, названа дзеркальною симетрією, яка вивчає такого роду збіги.
"Фізики робили дивовижні передбачення, а математики намагалися довести їх нашими власними засобами, - каже Бен-Цві. - Передбачення були дивними і дивовижними, і, як виявилося, вони практично завжди були правильними".
Але незважаючи на те, що КТП успішно генерує зачіпки для математики, її основні ідеї все ще перебувають за межами математики. Квантові теорії поля не є об'єктами, які математики розуміють досить добре, щоб використовувати їх як, наприклад, поліноми, групи, різноманіття та інші стовпи цієї дисципліни.
Для фізиків віддалений зв'язок із математикою є ознакою того, що їм ще багато чого потрібно зрозуміти про теорію, яку вони породили.
"Кожна інша ідея, яку використовували у фізиці протягом останніх століть, мала своє природне місце в математиці, - каже Зайберг. - З квантовою теорією поля справа йде явно інакше".
Математикам здається, що зв'язок між КТП і математикою має бути глибшим, ніж випадкова взаємодія. Це тому, що квантові теорії поля містять безліч симетрій, які диктують, як точки в різних частинах поля співвідносяться одна з одною. Ці симетрії мають фізичне значення - вони описують, як, скажімо, у часі зберігається енергія під час еволюції квантових полів. Але вони також є математично цікавими об'єктами самі по собі.
"Математика може породити певну симетрію, а ми можемо помістити її у фізичний контекст. Це створює прекрасний міст між цими двома галузями", - каже Кастро.
Математики вже використовують симетрії та інші прийоми геометрії для вивчення широкого спектра проблем - від розв'язання різних типів рівнянь до розподілу простих чисел. Часто геометрія кодує відповіді на питання про числа. КТП пропонує математикам новий багатий тип геометричного об'єкта для гри - і зараз, за великим рахунком, невідомо, чи збережеться фізика як "повноцінна" наука.
"Якоюсь мірою ми граємо з КТП, - каже Ден Фрід, математик з Техаського університету в Остіні. - Ми використовуємо теорію як зовнішній стимул, але було б непогано, якби вона стала внутрішнім стимулом".
Дорожня карта КТП
Математика не приймає нові теми легковажно. Багато базових понять пройшли через довгі випробування, перш ніж посісти канонічні місця в цій галузі.
Візьмемо, приміром, дійсні числа. Математикам знадобилося майже 2 000 років практики, щоб дійти згоди в їхньому визначенні. Нарешті, у 1850-х роках вони зупинилися на точному виразі з трьох слів, що описує дійсні числа: "повне впорядковане поле". Вони повні, бо не містять пропусків; вони впорядковані, бо завжди є спосіб визначити, більше чи менше одне число стосовно іншого; вони утворюють "поле", тобто дотримуються правил арифметики.
"Ці три слова - історично важкі", - упевнений Фрід.
Щоб перетворити КТП на внутрішній стимул, математикам доведеться дати теорії таке саме пояснення, як і дійсним числам: чіткий список характеристик, що задовольняє будь-яку квантову теорію поля.
Велику роботу з перекладу частин КТП у математику виконав Кевін Костелло з Інституту Ватерлоо, Онтаріо, Канада. У 2016 році він написав підручник, який ставить пертурбативну КТП на міцну математичну основу, включно з формалізацією нескінченних величин, які з'являються під час збільшення числа взаємодій. Ця робота слідує за алгебраїчною квантовою теорією поля, яку Рейзнер розглянула у своїй книзі 2016 року. Хоча пертурбативна КТП не описує Всесвіт, математики знають, як впоратися з фізично несенсаційними нескінченностями.
"Його внесок надзвичайно винахідливий і проникливий. Він помістив теорію в нові красиві рамки суворої математики", - каже Мур.
Костелло пояснює, що написав книгу з бажання зробити пертурбативну квантову теорію поля більш послідовною.
"Я просто знайшов методи деяких фізиків невмотивованими і ситуативними. Мені хотілося чогось більш самодостатнього, з чим міг би працювати математик", - каже він.
Уточнивши, як саме працює теорія збурень, Костелло створив основу, на якій фізики та математики можуть будувати нові квантові теорії поля. Нову математику швидко прийняли інші фахівці в цій галузі.
Костелло також працював над визначенням того, що таке квантова теорія поля. В урізаному вигляді вона вимагає геометричного простору, де проводяться спостереження в кожній точці, у поєднанні з кореляційними функціями, які виражають, як спостереження пов'язані одне з одним. Робота Костелло описує властивості кореляційних функцій, підводячи їх до формальних вимог КТП.
Найвідоміші теорії, Стандартна модель приміром, містять додаткові властивості, не властиві для всіх теорій поля. Ймовірно, вони описують інші, ще не відкриті властивості. І тут криється методологічна проблема: як розрахувати те, чого немає або те, що невідомо?
"Існує великий ліхтарний стовп, під яким можна знайти теорії полів, а навколо нього - велика темрява, яку ми не розуміємо, як визначити, але знаємо, що вона є", - філософствує Гайотто.
Костелло висвітлив частину цього темного простору за допомогою низки визначень квантового поля. На основі цих визначень він відкрив дві нові квантові теорії поля. Жодна з них не описує наш чотиривимірний всесвіт, але вони задовольняють основним вимогам геометричного простору, оснащеного кореляційними функціями.
І якщо математика зможе визначити повний простір можливостей квантових теорій поля - усю множину різних можливостей для задоволення загального визначення, що містить кореляційні функції, - фізики знайдуть шлях до конкретних теорій, які слабо уявляються.
Завдання на кілька поколінь
Належить пройти довгий шлях. Досі всі квантові теорії поля, представлені в повному математичному вигляді, спираються на різні спрощення, які полегшують математичну роботу з ними.
Один із таких способів полягає у вивченні простіших двовимірних КТП, а не чотиривимірних. Нещодавно група дослідників із Франції з'ясувала всі математичні деталі двовимірної КТП.
Інші спрощення припускають, що квантові поля симетричні таким чином, що вони не відповідають фізичній реальності, але математично еквівалентні. До них належать "суперсиметричні" і "топологічні" КТП.
Наступним і набагато складнішим кроком буде математичний опис квантової теорії поля, який краще відповідає фізичному світу, точніше кажучи, геометрії, вибудуваній загальною теорією відносності Ейнштейна.

"Дуже незручно, що у нас немає жодної квантової теорії поля, яку ми могли б описати в чотирьох вимірах непертурбативно, - заявила Рейзнер. - Це важка проблема, і, очевидно, для її розв'язання знадобиться не одне і не два покоління математиків і фізиків".
Що, втім, не заважає математикам і фізикам метатися між невизначеним і доступним. Визначення характерних властивостей, спільних для всіх квантових теорій поля, майже напевно потребуватиме об'єднання двох стовпів математики: аналізу, що пояснює, як управляти нескінченностями, і геометрії, яка формалізує мову симетрії.
"Це захоплива проблема в самій математиці, тому що вона об'єднує дві великі ідеї", - каже Дейкграаф.
Якщо математики зможуть зрозуміти КТП, то невідомо, які відкриття чекають на нас у майбутньому. Математики давно визначили характерні властивості інших об'єктів, як-от різноманіття та групи, і тепер ці об'єкти пронизують практично кожен куточок цариці наук.
"Мені подобається говорити, що фізики не обов'язково знають усе, але фізика знає все, - стверджує Бен-Цві. - Якщо ви поставите їй правильні запитання, то в ній уже є явища, які шукають математики".
А для фізиків повний математичний опис КТП - це зворотний бік головної мети їхніх досліджень: повного опису фізичної реальності.
"Я відчуваю, що існує одна інтелектуальна структура, яка охоплює все, і, можливо, вона охопить усю фізику", - переконаний Зайберг.
Тепер математикам залишається тільки розкрити її.
Джерело: Quanta Magazine










