Команда фізиків з Політехнічного інституту Вірджинії, США, запропонували новий погляд на те, як геометрія простору-часу пов'язана з гетеротичною теорію струн. Остання вважається “провідним кандидатом” на єдину теорію квантової гравітації.
Стаття опублікована в журналі Physical Revew D і провокує широку дискусію навколо ролі калібрувальних полів, 5-бран та гравітаційних аномалій.
Теорія струн - це свого роду теоретична платформа, що намагається математично описати всі фундаментальні сили і частинки з альтернативної точки зору, трактуючи мікрооб’єкти як крихітні вібруючі струни у вищому вимірі простору-часу.
Однак фізикам-теоретикам не вдається чітко визначити додаткові (до чотирьох відомих) виміри, хоча вони стверджують про згортання таких вимірів у форми, сумісні зі спостережуваним чотиривимірним всесвітом.
На цю мить найбільш відома геометрія Калабі-Яу (ГКЯ) шестивимірного простору з особливими властивостями симетрії.
Крім ГКЯ, пропонуються інші варіанти геометрій, але поки незрозуміло, як вони пов'язані одна з одною. Тому виникає необхідність переписати топологію “струнного” простору й подивиться, чи працює математика. Якщо формули та графіки сходяться та не конфліктують між собою, тоді можна переходити до іншого кроку - визначити параметри до сингулярної межі та критерії розв'язання сингулярності.
Науковці в цьому випадку обрали коніфолд-перехід - геометричний перехід, що замінює конічну сингулярність на гладку двосферу, хоча й не проти флоп-перехуду з заміною сингулярної кривої на іншу, “доступну” криву.
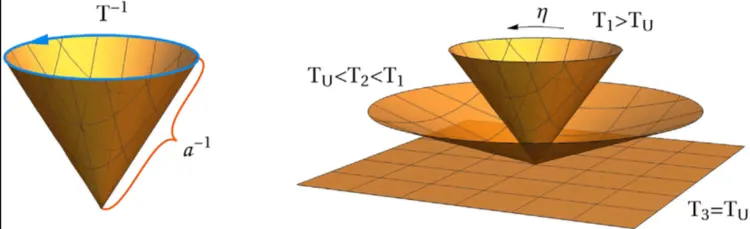
Геометричні переходи інтенсивно вивчалися в контексті N=2 суперсиметричних теорій у чотирьох вимірах, тобто за спрощеною версією теорії струн. Однак реалістичні теорії струн мають N=1 суперсиметрію, - аналітично вона набагато важча з точки зору математики або фізики.
Зокрема, в гетеротичної теорії струн геометрія компактифікації не є “монопольним” інгредієнтом: калібрувальні групи симетрії дозволяють кодувати електромагнетизм та сильну ядерну взаємодію.
Крім того, можуть бути й інші непертурбативні елементи, такі як NS5-брани - протяжні об'єкти, що обертаються навколо деяких циклів ГКЯ.
Наявність цих додаткових особливостей ускладнює вивчення геометричних переходів, оскільки вони вводять нові джерела сингулярності та аномалій, тобто невідповідностей, яких треба уникати або скасовувати. Іноді доводиться мати справу не лише з сингулярною геометрією, а й з поведінкою 5-бранів на сингулярній геометрії.
Також деякі з цих сингулярностей можуть знаходитись поза межами звичайної теорії поля і вимагати більш екзотичних інструментів, на кшталт струн без натягу або суперконформних секторів.
Автори дослідження стверджують, що ключем до конічного переходу може бути процес створення пар, де 5-брани виникають одночасно в калібрувальному та гравітаційному секторах, а потім поглинаються у голоморфний котангенціальний та фоновий калібрувальний пучок, відповідно.
Таким чином змінюється топологія інваріантів, а відповідно, кривизна простору. Інакше кажучи, існує вірогідність виникнення нових фізичних властивостей, але у “згорнутому”, 4-вимірному представленні.
Пропозиція американських вчених зберігає безмасовий спектр теорії, а також відтворює геометрію дуальності простору, пов'язуючи різні калібровані лінійні сигма-моделі у двох вимірах. Крім того, автори обговорюють обмеження та наслідки свого підходу і пропонують можливі напрямки майбутніх досліджень.
Уточнимо, що теорію струн навіть не можна вважати "повноцінною" фізичною теорією. Перед нами розгортається фундаментальна спроба математичного осмислення всесвіту, де фізичні об'єкти підміняються об"єктами математично. Поки що струнна "теорія" - математична абстрактна конструкція.
Фізичні ж теорії мають онтологію (фізичні речі, які насправді існують) та експериментально доведені або спростовані передбачення. Але розмірковування на тему бран та інших складних математичних об'єктів не пропонує зв'язок з реальністю, щоб ми під нею не розуміли.
З іншого боку, поки ми не розробимо математичний апарат "нової фізики", говорити про виникнення альтернативної фізичної теорії дуже важко. І в цьому сенсі дійсно краще експериментувати з математичними сутностями, щоб зрозуміти - чи є у нас вихід на онтологію природи.
